Раздел: Документация
0 ... 45 46 47 48 49 50 51 ... 96 2.2.3. Таблицы принятия решений (таблицы соответствий) Табличные модели весьма распространены в науке и технике. Во многих задачах проектирования мы имеем дело с 1.множеством решений (вариантов). 2.множеством условий, влияющих на выбор решения. Каждое условие в свою очередь принимает некоторое множество значений. Количество независимых условий, влияющих на выбор решений, может быть достаточно велико. Количество значений каждого условия также может достигать больших величин. Таким образом, общее количество значений условий, равное прямому (декартову) произведению множеств независимых условий, достигает весьма больших величин. Разработан специальный метод решения таких задач, названный методом поиска решений с помощью таблиц соответствий. Примеры: Необходимо выбрать: 1)план обработки поверхности: У =План обработки = f(X - вид поверхности, Х2 - точность обработки, х3 - шероховатость, Х4 - габариты поверхности); 2)сборочный робот: У =Робот = f(X\ - вид движения, Х2 - точность движения, х3 - вес детали); 3)гидропривод: У =Гидропривод = f(X\ - max скорость, Х2 -min скорость, х3 - усилие, Х4 - тип гидросистемы). У - множество решений. Y={yl})l = \ik. X - условия. X={X1,X2,Xy,Xm},y = l,m. Х={ХХ х X2x...X;x...Xw X ={Xji.}, ij =l,wy, y = l,7w, nj - количество значений j-го условия. Соответствием называется следующий кортеж: r=(G,y,X),GczyxX, Г - соответствие, G - подмножество У х X - график соответствия (см. рис.2.17). у = f(x) или у = f(x) - функциональная зависимость (см. рис.2.18). х\\ *\2 х3\ х32 хзз Ъ y2 y3 yt y5 y6 y7 ys yg Рис.2.17. График соответствия между значениями аргумента и значениями функции 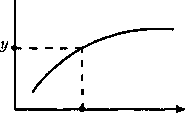 Рис.2.18. График функции Функция устанавливает соответствие между значением аргумента и значением функции. График функции - множество пар: график = {у>х1 Область определения X - декартово произведение непересекающихся независимых множеств. X = Х\ х X2X..xXw, Xj ={Xj\1Xj2,--.,Xjij1...1Xjmj). Каждое условие принимает nj значений, тогда X - множество m-оп вида, Х = {x\f\ >x2i2>-->xjij > - >xmim)\> i ~njy J -1*W. В терминах соответствий: X - область отправления, Y - область прибытия соответствия - множество возможных решений (см. рис.2.18.) Постановка задачи Задан некоторый кортеж: аР = А "*2i2»• • •»х jij »• • •»xmim )• Требуется найти У -образ, т.е. те решения, которые могут приниматься при данном наборе условий. Зададим связь между значениями условий и решениями в виде некоторого графа: Например, задан конкретный кортеж: ctp = (Х\%,Х2\, Х32) - выбор решения зависит, от третьего значения первого условия, от первого значения второго условия и от второго значения третьего условия. ctp =(Х1з,Х21 ,32) -> У*, У* - образ кортежа (решение). УОСхз) = {У2>Уз>У5У> У<*21 )={Уг>УА>УъУ> У(Х32) ={*/5>#8 >У*)\ У = ПХ13) п У(Х21) п У(Х32) = г/5. Возможны следующие варианты. 1.У - может быть одноэлементным множеством -¥ тогда решение единственное. 2.У - многоэлементное множество -¥ тогда имеем несколько вариантов решений. 3.У - пустое множество -¥ нет решений. Это говорит о том, что заданная система значений и условий несовместима с заданным множеством решений (см. табл.4). Таблица 4 Форма задания соответствия
Порядок заполнения таблицы принятия решений. 1.На основе анализа предметной задачи формулируется множество решений Y ~ {У\}»I - 1» и записывается в левый столбец таблицы соответствия. 2.На основе анализа предметной задачи формулируется множество условий, влияющих на решение , т.е. всего у нас т условий, влияющих на решения. 3.На основе анализа предметной задачи для каждого условия определяются множества значений этого условия. 0 ... 45 46 47 48 49 50 51 ... 96 |
|||||||||||||||||||||||












