Раздел: Документация
0 ... 76 77 78 79 80 81 82 ... 166 Замечание! Если коэффициенты не зависят от температуры, то нет необходимости заполнять поле Temperatures. ЗАДАЧИ МЕХАНИКИ ТВЕРДОГО ТЕЛА Основные понятия Механические свойства материалов Обычные детали (твердые тела) обладают комплексом свойств: тепловыми, механическими и др. В этом разделе рассмотрим механические свойства материала. Различные материалы ведут себя по-разному при различных уровнях нагрузки, т.е. в каком-то диапазоне напряжений определенный материал ведет себя как линейно-упругий, в другом диапазоне он деформируется пластически и т.д. (различия будут рассмотрены ниже). В то же время, другой материал может практически во всем диапазоне нагрузок вести себя как нелинейно-упругое тело. Если при этом учесть, что границы диапазонов меняются в зависимости от температуры, то становится очевидным, что установить универсальный закон деформирования для всех материалов невозможно. С другой стороны, все эти особенности поведения материалов привели к тому, что в настоящее время применяются различные модели для описания связи напряжений и деформаций при различных условиях. Следует отметить, что при решении задач механики сплошной среды, инженер часто отвлекается от неоднородности материала. Это оправдано тем, в подавляющем числе практических задач представляет интерес не поведение каждой молекулы (атома), а общее состояние тела. Инженер, заранее зная, что именно ему необходимо исследовать для какой-либо конструкции в рамках реального диапазона нагрузок, делает предположение о характере деформирования ее элементов. И таким образом выбирает, какая физическая модель деформирования будет использоваться. При этом для получения конкретного результата, инженер должен определить численные значения ряда физических параметров, характерных для выбранной модели. Кратко рассмотрим основные возможности ANSYS при использовании тех или иных моделей и способов задания соответствующих констант. Понятие о тензоре напряжений Как известно из курса сопротивления материалов, детали меняют свои размеры и форму (деформируются) под действием внешних сил. В них возникают внутренние усилия, величина и распределение которых зависит от действующей нагрузки и геометрической формы тел. Рассмотрим деталь произвольной формы, находящуюся в равновесии, под действием внешних нагрузок (рис. 213). Предположим, что воображаемое сечение плоскостью ZOY делит тело на два объема - V\ и 2 • Можно условно отбросить один из объемов, заменив его действие соответствующими усилиями на поверхности сечения. В нашем случае в окрестности с площадью AS любой точки А поверхности сечения действуют сила, величиной АР, и момент, величиной AM. Будем предполагать, что направление нормали в точке А и направление действия силы АР совпадают (в общем случае это не так). Кроме того, положение системы координат выбрано так, что направление вектора нормали v к поверхности сечения (граница объема К2) в данном случае совпадает с единичным направляющим вектором ех оси ОХ. 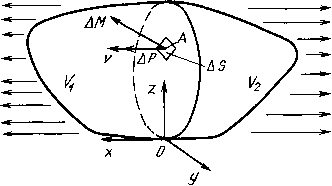 Рис. 213. Сечение твердого тела с приложенными нагрузками Тогда можно определить вектор напряжений, действующих в точке А вдоль нормали v: В соответствии с частными предположениями, сделанными выше (см. рис. 213), получаем, что в данном случае ov =ох. Таким образом, определяется напряжение, действующее на площадку, перпендикулярную оси ОХ. Отметим, что если напряжения положительные, то в данной точке тела происходит растяжение вдоль выбранной нормали, а если отрицательные - то сжатие. Напряжения в точке в направлениях вдоль осей OY, OZ глобальной системы координат определяются аналогично. Однако следует отметить, что в пространственном случае, для удобства вокруг точки А, находящейся в объеме тела, вырезается прямоугольный параллелепипед, грани которого перпендикулярны осям глобальной системы координат, а ребра параллельны им и имеют малые длины (рис. 214). При этом нормальные напряжения (напряжения, действующие перпендикулярно выбранной грани) обозначаются о"индекС) индекс (в ANSYS обозначается 3П0СТфИКС), где индекс (постфикс) указывает в плоскости, перпендикулярно какой оси глобальной системы координат действует данное напряжение, например обозначается 3П0СтфИкс1> „остфиксг)- Они действуют уже не перпендикулярно, а в плоскости выбранной грани. При этом первый индекс указывает грань параллелепипеда, в которой действует касательное напряжение. Эта грань перпендикулярна указанному первым индексом (постфиксом) направлению глобальной системы координат, а второй уточняет направление, параллельно которому на выбранной грани действует напряжение, например oxz (в ANSYS - SXZ) (рис. 215). Учитывая условие симметричности о у = о у,-, получаем для любой точки А твердого тела 6 компонент тензора напряжений: axx,Oyy,ozz,GXy,GyZ,ozx. Либо, обозначив оси координат х\, Х2, хз, получим следующие компоненты: о") j,0"22>°"33012>°"23031 • (в ANSYS - SX). Касательные напряжения обозначаются о индекс 1,индекс2 (в ANSYS 0 ... 76 77 78 79 80 81 82 ... 166 |












