Раздел: Документация
0 ... 77 78 79 80 81 82 83 ... 166 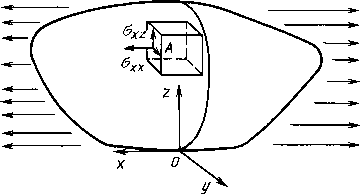 Рис. 214. Выбор элементарного прямоугольного параллелепипеда с центром в точке А твердого тела Без этих элементарных сведений трудно перейти к объяснению физических законов взаимосвязи деформаций и напряжений. Понятие о тензоре деформаций Если рассмотреть элементарный прямоугольный параллелепипед, находящийся в равновесии только под действием приложенных к его двум противоположным граням нормальных напряжений (например <зхх), то его длина в направлении действия нагрузки изменится по сравнению с размером до приложения нагрузки (увеличится, если приложенные напряжения являются растягивающими, или уменьшится, если напряжения - сжимающие). Это явление называется деформированием, а мера изменения размера - деформацией. Деформации определяют, в частности, относительное изменение размеров параллелепипеда вдоль осей системы координат и часто обозначаются в литературе ъхх,гуу,г22. Например, гхх =ALX/LX , где Lx - длина ребра параллелепипеда в направлении действия нагрузки до момента ее приложения, a ALX - изменение длины ребра в указанном направлении после приложения нагрузки (см. рис. 215). В ANSYS для Деформаций используется обозначение ЕРП0СТфикс, где постфикс указывает
Рис. 215. Элементарный параллелепипед с приложенными к его граням нагрузками на физическую модель, в которой данные деформации исследуются, а направление указывается отдельно. Кроме того, изменение прямых углов параллелепипеда под действием нагрузки обычно обозначается через гху, гуг, zxz. В последнем случае индексы указывают, в какой плоскости происходит сдвиг. Замечание! Отметим, что в ANSYS обозначение деформаций не зависит от направления (для одной и той же физической модели совпадают полностью), а направление в постпроцессоре описывается отдельной фразой. Аналогично компонентам тензора напряжений получаем шесть ком- понент тензора деформаций: е хх &уу £ ZZ &Ху » £yz 2 . Обозначив оси координатх\,х2, х3, получим следующие компоненты: £i ь е22, £33, £i2> £23, £31- Основные физические законы деформирования твердых тел Для решения задачи механики твердого тела необходимо установить физическую связь между деформациями и напряжениями, учитывающую особенности поведения материала детали (твердого тела), находящегося под воздействием внешних нагрузок. В разделе, посвященном решению задач твердого тела, рассматриваются следующие физические модели деформирования: •Линейное деформирование (упругость). •Нелинейное деформирование материала (нелинейная упругость, пластичность). Модель линейного деформирования при постоянной температуре. Общие сведения Традиционно наиболее широко используемой моделью является модель упругого линейного деформирования материалов (закон Гука). В рамках этой модели решается подавляющее большинство конструкторских задач. Объясняется это тем, что после снятия нагрузки любая деталь должна приобрести первоначальную форму. Это является залогом ее работоспособности в дальнейшем. Традиционно пояснение особенностей деформирования твердых тел осуществляется на хорошо известной зависимости напряжений от деформаций для цилиндрических образцов при одноосном растяжении. В рассматриваемом случае диаграмма имеет наиболее простой вид (рис. 216). Стрелками указывается направление изменения напряжений при увеличении (стрелка сверху) и уменьшении (стрелка снизу) деформации. Как видно из рисунка при упругом деформировании, деформация является обратимой, т.е. после снятия нагрузки деформация полностью исчезает. Вернемся к рисунку параллелепипеда с приложенными напряжениями (см. рис. 215). В рассматриваемом случае связь деформаций и напряжений в любом направлении системы координат подчиняется линейному закону. Дополнительно предположим, что при деформации вследствие действия на гранях только равномерно распределенных нормальных напряжений прямые углы эле-Рис- Ш- Зависимость напряжений от деформаций ментарного параллелепипеда не ис- rгпри одноосном растяжении •сажаются.образца  0 ... 77 78 79 80 81 82 83 ... 166 |
|||||||||||||||||||||












