Раздел: Документация
0 ... 47 48 49 50 51 52 53 ... 290 Поэтому расчетные сопротивления для поперечной и отогнутой арматуры R„v в уравнениях проекций на нормаль к оси элемента (5.37) принимаются пониженными (см. 3.6). В уравнении моментов (5.36) расчетные сопротивления не снижаются, так как плечи Zsw и zsj„c усилий, действующих в хомутах и отгибах, расположенных вблизи конца наклонной трещины, малы. Поэтому некоторая неточность значений моментов от усилий, действующих в этой арматуре, незначительно сказывается на величине суммарного момента. 5.3.1. Расчет наклонных сеченнй по поперечной силе Практические расчеты наклонных сечений по поперечной силе удобно производить по следующей методике. Если элемент армирован только продольной арматурой и поперечными стержнями (хомутами), то условие прочности можно представить в виде б(5-42) где Qbs - наименьшее значение поперечной силы, воспринимаемой совместно бетоном сжатой зоны и хомутами, пересекаемыми наклонной трещиной. Наименьшее значение Qbs в начале участка соответствует наиболее опасному наклону сечения, для отыскания которого составим следующее выражение (рис. 5.13): М QQbs = qico +«)+qmc0 +-(5 43) где q - равномерно распределенная внешняя нагрузка; qm - предельное усилие в хомутах на единицу длины элемента, равное R...A.. (5.44) я - расстояние между хомутами. Заметим, что для заданного элемента и нагрузки поперечная сила Qbs, определяемая формулой (5.43), является лишь функцией с0. Отыщем положение наиболее опасной наклонной трещины (длину ее проекции с0), на образование которой потребуется минимальная поперечная 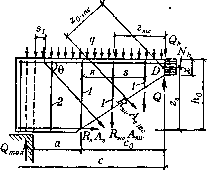 Рис. 5.13. К расчету прочности наклонных сечений: 1 - поперечные стержни, принимающие участие в работе; 2 - стержни, не пересекаемые трещиной сила Q. Для этого берем производную от Q по с0 и приравниваем ее нулю: dQМ, п -г = я+ч„-f = 0, dCoСо откуда (5.45) Полученное значение с0 принимается не более 2h0 и не более значения с (см. рис. 5.13), а также не менее h0, если c>h0. Подставляя найденное значение с0 в формулу (5.43), получим: Наименьшее значение Qbs будет приа=0, т.е. в наклонном сечении, проходящем у грани опоры: Qbs=2Mb(qsw+q).(5.46) Если подставить значение с0 из (5.45) в (5.38), получим выражение для поперечной силы, воспринимаемой бетоном сжатой зоны над наклонной трещиной: Сравнивая (5.47) и (5.46), отметим, что при наиболее опасном наклоне трещин поперечные силы, воспринимаемые бетоном сжатой зоны и поперечной арматурой, равны по величине и составляют половину Qbs. После подстановки в (5.46) значения Мь из (5.38) получим: Сплошная равномерно распределенная нагрузка g в пределах длины проекции наклонного сечения учитывается лишь в элементах, рассчитываемых только при одной схеме нагрузки, когда эта нагрузка действует постоянно (например, при гидростатическом давлении, давлении грунта, и т.п.). В большинстве случаев нагрузка q, уменьшающая величину поперечной силы, ввиду того что она может отсутствовать или перемещаться, в выражении (5.48) не учитывается. Значение Qb, вычисленное по формуле (5.38), принимается не менее q>bl(\+<pf + <pJRblbh0, где значения <рьз даны в табл. 5.3. При проектировании элемента, наметив диаметр поперечных стержней (хомутов) и расстояния между ними, определяют qm по формуле (5.44). Его значение должно быть не менее 0,5<рн(1 + <pf + <pn)Rblb. Найденное значение qm. подставляют в (5.48) и вычисляют Qbs, после чего проверяют условие (5.42). Если при этом расчетная поперечная сила Q> Qbs, т.е. условие (5.42) не удовлетворяется, на данном участке следует увеличить поперечное сечение хомутов или уменьшить расстояние между ними. При армировании балки вязаными каркасами из отдельных стержней избыток поперечной силы сверх величины Qbs целесообразно передавать на отогнутую арматуру. Необходимое сечение отгибов, располагаемых в одной наклонной плоскости: (5.47) (5.48) Л (5.49) 0 ... 47 48 49 50 51 52 53 ... 290 |












