Раздел: Документация
0 ... 74 75 76 77 78 79 80 ... 290 пряжения в арматуре превышают условный предел текучести. Рост напряжений после достижения в арматуре величины о0 2 зависит от характера диаграммы растяжения сталей (от отношения о"0>2/о"и). Так, стали классов A-IV и Ат-IV имеют более подъемную диаграмму растяжения за условным пределом текучести (более низкие значения а02 /а„), чем стали классов А-V, Вр-И, К-7, и, следовательно, относительно больший резерв роста напряжений после достижения величины а02. С уменьшением £ (или процента армирования) деформации растянутой арматуры к моменту разрушения сжатой зоны бетона увеличиваются. В элементах с арматурой, не имеющей площадки текучести, это ведет к одновременному увеличению напряжений. В нормах рост величины напряжения при £,<£,R учитывается умножением расчетных сопротивлений арматуры Rs на коэффициент ys6. Зависимость между YS6 и £ нелинейна, однако в целях упрощения в нормах принята линейная функция: У,6=п-(1-п)(2£/-1)£п,(8.23) где т] принимается равным для арматуры: классов A-IV и Ат-IV - 1,2; классов A-V, Ат-V, В-П, Вр-И и К-7 -1,15; А-VI и At-VI - 1,1. В формуле (8.23) значения £ и £я подсчитывают по расчетным значениям. Прочность нормальных сечений изгибаемых элементов при первом случае <£,R) рассчитывают по формулам (рис. 8.20): RA = у,«*А + RA - КЛ - о,с4Р.(8.25) где а5С - определяется по формуле (8.22); Ssp = Asp (/i0 -ар);ys6 - определяется по формуле (8.23); остальные характеристики имеют такой же смысл, что и в формулах (5.19) - (5.20). Зависимость напряжений в арматуре от относительной высоты сжатой зоны сечения При £ > E,R напряжения в арматуре растянутой зоны при разрушении элемента не достигают расчетного сопротивления (<3S < Rs). В этом случае для определения прочности элемента уравнений (8.24) и (8.25) недостаточно, так как в них вместо Ry следует подставлять третье неизвестное as. 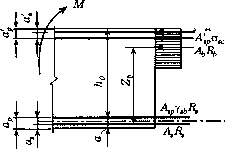 А Рис. 8.20. Схема усилий в поперечном сечении изгибаемого предварительно напряженного элемента при расчете на прочность При заданных классах бетона и арматуры деформации и напряжения в арматуре зависят от высоты сжатой зоны сечениях и расстояния арматурного стержня до сжатой грани hoi (рис. 8.21), т.е. от относительной высоты сжатой зоны = xlhot. 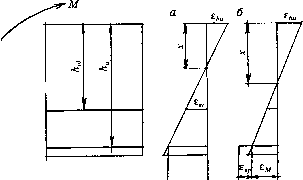 9е.е, Рис. 8.21. Схема связи деформаций арматуры с высотой сжатой зоны сечения: а - ненапрягаемой; б - предварительно напряженной При возрастании £ , что связано либо с увеличением высоты сжатой зоны.г, либо с уменьшением hoi, деформации и напряжения арматурного стержня понижаются и могут поменять знак. Если арматура предварительно напряжена, то часть деформаций, равных £sp , выбирается еще до воздействия внешней нагрузки (рис. 8.21, б). При одной и той же суммарной деформации арматуры предварительное напряжение ведет к увеличению высоты сжатой зоны от внешней нагрузки. Опыты показали, что в предельном состоянии (при разрушении сжатой зоны) связь между деформациями арматуры и относительной высотой сжатой зоны (условной, т.е. при прямоугольной эпюре напряжений в сжатом бетоне) имеет гиперболический характер и приближенно описывается эмпирической зависимостью: £„ = - ) + £ip"(8.26) где со - параметр, характеризующий сжатую зону бетона (см. формулу 5.5); sspj - деформация/-го стержня от предварительного напряжения с учетом потерь. На рис. 8.22 зависимость (8.26) графически представлена сплошной линией для элементов с ненапрягаемой арматурой (при espi = 0) и пунктирной для преднапряженных элементов. В первом случае деформации, отложенные по оси ординат, представляют собой деформации от внешней нагрузки, во втором (пунктирная линия) - суммарные от внешней нагрузки и предварительного напряжения. Принимая ею = es и умножая все члены уравнения (8.26) на модуль упругости арматуры, получим формулу для определения напряжений в арматуре при ее упругой работе: о\,. = - 1-± 1Д (8#7) где oicx -emEs - предельное напряжение в арматуре сжатой зоны. Поскольку переход от зависимости (8.26) к (8.27) совершен путем умножения всех членов на постоянную величину, их графическое изоб- 0 ... 74 75 76 77 78 79 80 ... 290 |












