Раздел: Документация
0 ... 88 89 90 91 92 93 94 ... 290 вым, который ввел в расчет факторы, учитывающие реальные физические свойства железобетона, в частности участие в работе бетона растянутой зоны на участках между трещинами, наличие неупругих деформаций бетона сжатой зоны и др. Этот метод расчета в последние годы значительно усовершенствован и распространен на предварительно напряженные, внецентренно сжатые и внецентренно растянутые элементы при кратковременном и особенно при длительном действии нагрузок. При изгибе элемента растянутая зона делится трещинами на участки длиной 1СГС. Наибольшие напряжения (деформации) в растянутой арматуре os{es) и в сжатом бетоне оь(еь) возникают в сечениях с трещинами, где бетон растянутой зоны выключается из работы. По мере удаления от трещин напряжения (деформации) убывают (рис. 9.6). Отношение средних напряжений (деформаций) арматуры на участке между трещинами к максимальным в сечении с трещиной представляет
Рис. 9.6. Изменение напряжений на участке между трещинами: а - схема изгибаемого элемента; б - эпюры растягивающих напряжений; в - касательные напряжения на поверхности контакта арматуры и бетона собой коэффициент y/s (см. формулу 3.9). Графически этот коэффициент можно представить как отношение площади эпюры напряжений в арматуре на участке между трещинами ко всей площади эпюры напряжений О" / - СЫО" ,/ , О", где <js2 = <js -<Jsi - разность напряжений в арматуре в сечении с трещиной и посередине между трещинами; со - коэффициент полноты эпюры растягивающих напряжений, передающихся на бетон. Средние относительные деформации продольной растянутой арматуры esm и бетона сжатой зоны еЬт равны: Исходной формулой для расчета деформаций является выражение кривизны оси элемента 1/г, которое можно записать в виде (рис. 9.7, а): / £/+£./ crc sm crc bm сгс или А. (9.56) Раскроем содержание уравнения (9.56). Рассмотрим наиболее общий случай, когда на элемент действует изгибающий момент совместно с продольной сжимающей силой Ntol под которой можно понимать сумму равнодействующей внешней продольной силы N и усилия предварительного обжатия Р с учетом всех потерь: N,0I=P±N.(9.57) Определим средние относительные деформации растянутой арматуры еш и сжатой грани бетона еЬт. В сечении, проходящем через трещину, в стадии II в арматуре действуют напряжения as, а в бетоне - <зь. Обозначим через Ms (заменяющий момент) момент относительно оси, нормальной к плоскости изгиба и проходящей через центр тяжести арматуры растянутой зоны от всех внешних усилий (включая усилие Р), приложенных по одну сторону сечения (рис. 9.7, б). Для изгибаемых пред- 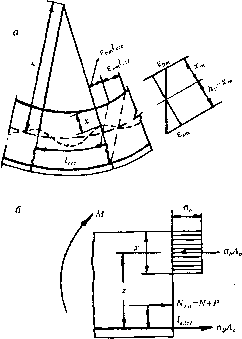 Рис. 9.7. К определению кривизны элемента напряженных элементовМ =M+Pesp, где esp - расстояние от линии действия усилия Р до центра тяжести площади сечения арматуры S, а для изгибаемого элемента из обычного железобетона (при отсутствии продольной силы) MS=M. Вводя в расчет заменяющий момент вместо изгибающего, мы «переносим» равнодействующую продольных усилий Ntm в центр тяжести арматуры растянутой зоны. Поэтому усилия в сжатом бетоне и растянутой арматуре соответственно будут равны MJz и MJz-Nlol, где г - расстояние от центра тяжести растянутой арматуры до точки приложения равнодействующей усилий в сжатой зоне сечения над трещиной. Напряжения в сжатом бетоне и растянутой арматуре получим, разделив соответствующие усилия на плопдадь сечения сжатого бетона Аь и растянутой арматуры As: 0 ... 88 89 90 91 92 93 94 ... 290 |
||||||||||||||||||||||||












