Раздел: Документация

0 ... 66 67 68 69 70 71 72 ... 119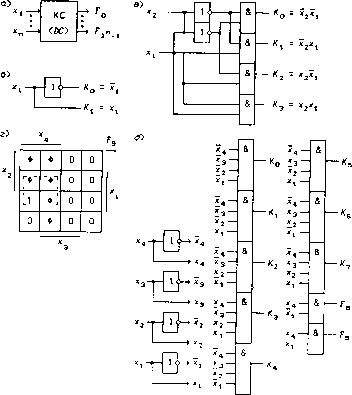

Рис. 6.1

пускаются только дешифраторы 4 х 10. Если подача на входы дешифратора кодов, идентифицируемых числами г = 10... 15, запрещена (табл. 6.1), то минтермы А8 и А9 можно заменить на функции F8 = х4х\ и F9 = х4Х\, реализуемые на двухвходовых ЛЭ И (минимизация функции F9 показана на рис. 6.1,г). Для соблюдения условия F, • Fj = 0 при г / j следует взять

Fi = Ki = x4xl3xl2xe11, г = e3e2ei = 0... 7.

Одна из возможных реализаций DC 4 х 10 на ЛЭ показана на рис. 6.1,д. В дальнейшем выходы DC независимо от их реализации будем обозначать через F,.

На рис. 6.2 приведены условные графические обозначения дешифраторов 4 х 10, изготовляемых в стандартных ТТЛ и КМОП сериях. В левом дополнительном поле указываются веса

Таблица 6.1. Таблица истинности дешифратора 4 X 10

г	14x3x2x1				Fo Fi F2 F3 F» F5 F6 F7 F8 F9
0	0	0	0	0	1	0	0	0	0	0	0	0 0 0
1	0	0	0	1	0	1	0	0	0	0	0	0 0 0
2	0	0	1	0	0	0	1	0	0	0	0	0 0 0
3	0	0	1	1	0	0	0	1	0	0	0	0 0 0
4	0	1	0	0	0	0	0	0	1	0	0	0 0 0
5	0	1	0	1	0	0	0	0	0	1	0	0 0 0
6	0	1	1	0	0	0	0	0	0	0	1	0 0 0
7	0	1	1	1	0	0	0	0	0	0	0	1 0 0
8	1	0	0	0	0	0	0	0	0	0	0	0 1 0
9	1	0	0	1	0	0	0	0	0	0	0	0 0 1
10	1	0	1	0	Ф	Ф	Ф	Ф	Ф	Ф	Ф	Ф ф Ф
11	1	0	1	1	Ф	Ф	Ф	Ф	Ф	Ф	Ф	ф ф Ф
12	1	1	0	0	Ф	Ф	Ф	Ф	Ф	Ф	Ф	ф ф Ф
13	1	1	0	1	Ф	Ф	Ф	Ф	Ф	Ф	Ф	Ф ф Ф
14	1	1	1	0	Ф	Ф	Ф	Ф	Ф	Ф	Ф	ф ф Ф
15	1	1	1	1	Ф	Ф	Ф	Ф	Ф	Ф	Ф	ф ф Ф

сигналов xp, равные 2P , а в правом дополнительном поле - числа t = еп...ер...е\. Это позволяет однозначно определить номер выхода с активным уровнем сигнала по двоичному числу, подаваемому на вход дешифратора. Интегральные схемы на рис. 6.2 выполняют функции:

155ИД1, 7441 - DC 4 х 10, имеющие выходы F, = А, с открытым коллектором (Voh < +60 В и 4-55 В);

555ИД6 - DC 4 х 10 с инверсными выходами Fi = Kf,

555ИД10, 7445, 74X5445 - DC 4 x 10 (выходы Fi = A\ с открытым коллектором; Voh < +15 В, IOL < 80 мА - 555ИД10 и 7445, Voh < +7 В - 74X5445);

561ИД1, 74ЯС4028 - DC 4 х 10 (по выходам F8 и F9 реализуются не минтермы, а функции х4х\ и х4х\ соответственно; ИС выполняет функции дешифратора 4 х 10 с запретом подачи на вход двоичных чисел г - е4е-$е2е\ = 10 ... 15).

Дешифраторы 4 X 10 с открытым коллектором можно использовать для реализации любой функции трех переменных х3, г2 и ii, если положить х4 = 0, так как в этом случае дешифратор реализует все минтермы трех переменных. На рис. 6.3 показана схема, выполняющая функцию

/(!/) = К0КзК4К6 = К0 V A3 V К4 V А6

---

155ИД1/41

		щ
	DC	°?
1
2		26
4		3 ?
8		4?
		54-
		еу
		7у
		8 Г
	141

555ИДВ

		F 1
	DC	06
1		1 6
2		2 i
4		3 4
8		46
		56
		6 4-
		76
		86
		9 4-
	41

555ИД10/45, LS445

12 - GA>D,3

GA>D,is

	->	Fj>
	DC	°T
)		1 4
2		2r
4		3 T
8		46
		5T
		6T
		7T
		86
	143

561ИД1, -4028 з

		F
1	DC	0
I 2		1 2
4		3
8		4
		5
		6
		7
		8
	4028	9

«4

«e

«7 f8

F9

СЛФ,16 - V

в - GA>D,is

Г

		2
	DC	F
1		0 •
2		1 <
4		2<
8		3i
		4 <
		5
		6 i
		7i
		8 <
		9 6

/CiO

Рис. 6.3

Рис		6.2 381ИД1
				F
			DC	0
*1 -		1		1
*2~		2		2
*з-		4		3
*4		8		4
				5
				6
				7
				8
				9

-EH

Рис. 6.4

		F
	DC	0	-
1		1	-
2		2	-
4		3	-
8		4
		5
		6
		7
		8
		9

(при значении Л", = 1, i = 0,3,4 или 6 функция / = 0). Эта функция имеет МДНФ

f(v) = х3хх V х2хх V X3X2X1, что требует большего числа корпусов ИС.

В общем случае (при любом значении числа переменных п) реализуемая по данному методу функция f(u) описывается выражением

2"-1

1=0

где i, - номера тех точек, в которых функция f(v) = 0.

Как следует из соотношения (6.1) для значений г = 0,1,..., 7, функции F{ = Х4Х33хе22Xj1, поэтому при подаче на один из дешифраторов 4 х 10 сигнала х4, а на другой - сигнала х4, получим дешифратор 4 х 16 (рис. 6.4), описываемый функциями

F, = xe*xl3xeJxV

i - c4c3e2ei = 0 ... 15.

6.2. Демультиплексоры

Демулътпиплексором (рис. 6.5,а; DMX - Demultiplexer) называется КС, выполняющая функции

Fi = E-Kt(v) = E-f[xep>,(6.2)

где Е - коммутируемый (демультиплексируемый) на один из 2" выходов сигнал, i = еп ... ех = 0 ... 2™ - 1. Действительно, если Ki(v) = 1, то Fi - Е, а если K{(v) = 0, то F, = 0. Совокупность значений сигналов и = (хп,...,х\) определяет адрес (номер) выходного канала, к которому подключается сигнал Е.

КС CDA0O

б)

Д1

- F,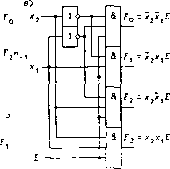

Сх .....х,~)

Рис. 6.5

Рис. 6.6

Демультиплексоры, имеющие п адресных сигналов хр, называются демулътиплексоралш 1 -> 2". Из сравнения (6.1) и (6.2) видна связь между дешифраторами n X 2™ и демульти-плексорами 1 -► 2": если положить £ = 1, то демультиплексор 12" превращается в дешифратор п х 2™. На основании (6.2) может быть построена схема демультиплексора при любом числе п адресных сигналов хр. Демультиплексор 12 (рис. 6.5,6) выполняет функции Fq = е • Х\ и F\ = е х\. На рис. 6.5,в показана схема демультиплексора 14. Если ЛЭ И заменить на ЛЭ И-НЕ, то получится демультиплексор 1 -► 4 с инверсными выходами. На рис. 6.6 изображена электромеханическая модель демультиплексоров 1 -> 2™, поясняющая принцип их работы.

Демультиплексоры могут быть описаны и с помощью таблиц истинности типа табл. 6.2, задающей демультиплексор 1 -» 8 с инверсными выходами DO{. Однако такой способ описания демультиплексоров и многих других цифровых узлов слишком

---

Таблица 6.2. Таблица истинности DMX 1-»-8

i	Е	«3*2*1	DO	7D06	DObD04D03D02DOi	DO0
0	1	ООО	1	1	11111	0
1	1	0 0 1	1	1	11110	1
2	1	0 1 0	1	1	1110 1	1
3	1	0 1 1	1	1	110 11	1
4	1	1 0 0	1	1	10 111	1
5	1	1 0 1	1	1	0 1111	1
6	1	1 1 0	1	0	11111	1
7	1	1 1 1	0	1	11111	1
-	0	XXX	1	1	1 1 1 11	1

громоздок по сравнению с аналитическим методом описания их законов функционирования, которому и отдается здесь предпочтение.

Интегральные схемы демультиплексоров. На рис. 6.7

приведены обозначения выпускаемых демультиплексоров 1 - 2™ (п = 2,3,4). Коммутируемый на 2™ выходов сигнал Е может представлять собой конъюнкцию нескольких сигналов Е3: Е = Е2Е\ и Е - Е3Е2Е\. Обозначения в адресной части дополнительного левого поля и в правом дополнительном поле полностью соответствуют обозначениям, принятым для дешифраторов 4x10 (рис. 6.2).

На рис. 6.7 представлены демультиплексоры: 1533ИДЗ, 74ЛСТ1154 - DMX 1 -»• 16 с инверсными выходами Fi, выполняющие функции

Fi(v) = Е Ki(v) = E-x\*x%xe*x\l, Е = ЕХЕ2, i = e4e3e2eV,

1533ИД19 - DMX 1 -v 16 (инверсные выходы Fi с открытым коллектором);

555ИД4 - сдвоенный DMX 1 -> 4 с инверсными выходами F и F", представляющий собой два DMX 1 -< 4 с общими адресными сигналами х2 и х\.

F = E-Ki{v) = E2Ex\\ \ if = G • Ki(v) = G2GlX?x?; J

555ИД5 - сдвоенный DMX 14, имеющий инверсные выходы Fi с открытым коллектором;

1533ИД7, 74ЛС11138 - DMX 1 -+ 8 с инверсными выходами, Е = Е\Е2Е3;

531ИД14, 561ИД7, 74ЛС11139 - два DMX 1 4 с инверсными Fi выходами;

153ЭИДЗ

153ЭИД19

ЛС11154

НС238

5J

		F
	DMX	0 4-
1		1 <f
2		2 4-
4		3 T
8		ч 64 74 84 94 104 114
		124 134
4 1		14 4
2	134	15 4

gnd, 24 555ИД4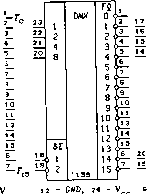

		F
	DAK	of
1		1 f
2		2 f
4		3 f
8		4f
		5<r
		6 4-
		8 f
		9 4
		10 4
		11 4
		12 4
&£		13 у
\		14 4
2		15 4

			F
l	1	DAW	0
2	2		1
3	4		2
			3
	&£		4
4,	. 1		5
3	) 2		6
б	3		7
8	- ghd,is		- V

OCX 1138

555ИД5

&E		f
> 1	DMX	0 i
2		l <
		2 )
1		3 i
2		F
		0 <
&G		1 <
> 1		2 (
I 2		3 <
T	133

&E > 1 2	DMX	n\ 0i 1J 2J
1		3 (
2		Ffi 0 с
&C V	1 3S	1< 2( 3<

GND, is 1533ИД7

8 - 6A/D, 16 15Б1ИДВ,HC239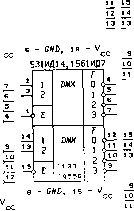

		F
1	DMX	0 4-
2		1 4
4		2 4
		3 4
&E		4 4
i 1		5 4
\ 2		6 4
3		7 4

4 - gnd,12 -ДС11238

		F
1	DMX	0
2		1
4		2
		3
&£		4
. 1		5
} 2		6
1 3		7

		F
1	DMX	о 4
2		l 4
4		24 34
&£		4 4
> 1		5 4
\ 2		6 4
3	138	7 4

gnd, is - Vc t E = Е,Е,ЕЯ

1 2	DMX	F 0 1 2 3
. E
1 2	DMX	F 0 1 2
Г	4333	3

ДС11139

4 - GA>D, 12 - V. ДСП 239

e - CM), is

£3-

r

DMX

DMX

DMX

DMX

4 - gnd, 12 - V

gnd,12

0 ... 66 67 68 69 70 71 72 ... 119