Раздел: Документация
0 ... 86 87 88 89 90 91 92 ... 119 а) =1 QJefJ -J.P =1 J.p»l J CR- - D ОС j к другим I разрядам JCl 4032В 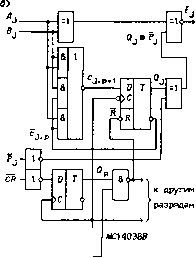 CR [~" «я. r " V F. : 0 r№№Jiriru u 4-=-+ -I-h j I JF~il° i" i -hr-h Op r 4-I- LJlJlJTJiririrU 29 = -103 -A 1LJT LTUl о □ -I-у +3B - 109 555ИМ7 - четыре последовательных сумматора-вычитателя с общими тактовым сигналом и инверсным асинхронным потенциальным сбросом R; МС14032В - три последовательных сумматора для прямых операндов с управлением сигналом Pj полярностью выходов Fj, имеющие общие тактовый сигнал и прямой квазисинхронный сигнал сброса CR; МС14038В - три последовательных сумматора для инверсных операндов с управлением сигналом Pj полярностью выходов Fj, имеющие общие тактовый сигнал и инверсный квазисинхронный сигнал сброса СR. Сумматоры 555ИМ7 описываются функциями Q\j = (AjdH V QAjdH) R, Q%2 = (BjdH V QBjd~R) R, n+ =1 (°+ldH V QcjdHyR при SBj = 0, 4cj \ Ry Cj,p+1dR V QcjdB при SBj = 1, Cj,p+i = QajQbj v QajQcj v QbjQcj, Sj = Qaj © Qbj e Qcj © SBj, где Cj,p+i - перенос в следующий разряд, Qcj = CjiP - перенос в данный разряд, SBj - сигналы управления операциями сложения и вычитания (SBj = 0 - сложение, SBj = 1 - вычитание), j = 1,2,3,4. Структурные схемы сумматоров МС14032Б и МС14038В и временные диаграммы, поясняющие их работу, показаны на рис. 6.112,а,6. Различаются эти схемы активным уровнем суммируемых разрядов Aj и Bj (прямые значения на рис. 6.112,а и инверсные - на рис. 6.112,6), а также фронтом тактового сигнала, по которому срабатывают триггеры сброса и переноса. Оба сумматора описываются функциями» Q+ = CR-dB V QRdB, R = QRB, Qt = (Cj<p+1dB v Qj~M)-R, cS,p+i = AjBjVAjQjVBjQj, Fj = Aj © Bj © Qj © Pj = Sj © Pj, где R - сигнал сброса триггеров переноса, Cj,p+i - перенос в следующий разряд, Qj = CjiP - перенос в данный разряд, Sj = Aj ф Bj ф Qj - сумма разрядов, Pj - сигнал управления полярностью выхода Fj, j = 1,2,3. Числа Aj и Bj подаются на сумматоры в последовательном дополнительном коде, а значит, и сумма Sj представлена в этом же коде. 6.11. Арифметическо-логические устройства Арифметическо-логические устройства (АЛУ) широко используются для построения арифметических узлов, в частности, АЛУ является составной Частью любого микропроцессора. В отличие от сумматоров АЛУ выполняют не только арифметические, но и логические операции над n-разрядными операндами X = x„ i . ..xix0 и У = 2/„ i. - - 3/12/0- Логические операции над операндами производятся поразрядно: X = in i .. .ii 10, У = Уп-1 • • -УгУо, X * У = (zn i * 2/n i)... (хг * yi ){х0 * уо), где "*" - некоторые двухместные операции алгебры логики. 1533ИПЗ/Д5В81Л/Л51181564ИПЗ СР401818 УК1П814 1СП8В1 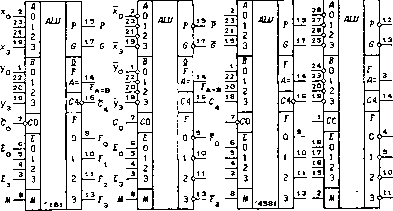 ,2 - GND. 24 - V12 - GND.24 - V„ s-9 - GMD 00, DD 21.22 - V Рис. 6.113 Арифметическо-логические устройства. На рис. 6.113 показаны ИС: 1533ИПЗ, 74Л5881Л и 74Л51181 - 4-разрядные АЛУ, изготовляемые по ТТЛШ-технологии (выход цифрового компаратора Fa= = Fa=b выполнен с открытым коллектором); 564ИИЗ,С£>40181Я, 74ЛС11181 и 74АС\ 1881 - 4-разрядные АЛУ, изготовляемые по КМОП-технологии. Для АЛУ 1533ИПЗ, 74Л5881 и 74Л51181 на рис. 6.113 приведены два графических обозначения, соответствующих использованию прямых и инверсных операндов: X = хъХ2Х!Хо, У = 2/32/23/12/0, F = F3F2FiF0; X = x3x2xiXo, У = ЪЪУхУо-, F = F3F2FiFo. Все АЛУ по выходам F, (t = 0,1,2,3) и FA= выполняют одинаковые арифметические и логические операции. Арифметические операции задаются значением сигнала М = О (М - Mode - режим), а логические операции - значением М = 1. Выбор одной из арифметических или логических операций задается кодом Е = E3E2EiEQ. В АЛУ реализованы все 16 воз-можных логических операций над двумя переменными. При выполнении арифметических операций АЛУ представляет собой 4-разрядный сумматор с параллельным переносом, имеющий дополнительные сигналы G и Р, используемые для параллельного каскадирования 4-разрядных секций. Рассмотрим принцип построения АЛУ 1533ИПЗ (рис. 6.113) с инверсными сигналами переносов со, с4 и прямыми операндами А", У и F. Из выражений (6.42) следует, что с,+1 = х{у{ V XiCi V у.с, = ij, V р{С4, Si=p~i® д{ ф с,-, где <7, = z, yt, р, = ii V у,. Тогда переносы с, можно представить в виде: с\ = д~о v Роо, с2 = V рхсх = дх V р{д0 V р,р0с0, Ъ = д2У р2с2 = д2м р2дх v p2Piffo v ЪПРоёо, f4 = «3v Рзз = Из v P3V2 v P3P2ffi v РзРгРхдо v P3P2PiPo?o, c4 = G V P • c0,(6.55) G = g3 V p3g2 V p3p2gx V p3p2pxg0, P = P3P2PiPo- (6.56) Чтобы сумматор выполнял и логические операции, вместо [разрядов ж, и у, чисел А и У следует использовать некоторые функции /,• = fifr,yi) и щ = <pi(xi,yi), а это дает = J.ft, >,- = /, V Тр{. Если взять /, = х{у{Е3 V Xiy{E2 и <р{ = х{ V 2/,£i V y,£0, To функции </,-, Pi и Si = i- можно представить в форме 9i = = х{ V j/,£i V у{Ео, р{ = 7,- V ft = ar,-y,-£* V г,-у{£2, = (ж,у,£3 V z,y,£2) Ф (xi V y, V y,£0) Ф (с, V A/), (6.57) (6.54) Таблица 6.23. Функции, выполняемые АЛУ
Таблица 6.24. Сравнение чисел с помощью АЛУ*
где Ез, Е2, Ei, Ео - сигналы выбора одной из 16 операций, М - сигнал выбора логических или арифметических операций. Принципиальная схема АЛУ 1533ИПЗ выполнена в соответствии с соотношениями (6.54) - (6.57), и добавлением функции 4-разрядного цифрового компаратора: з Fa=b = П Я- 1=0 Перенос с4 используется при последовательном включении нескольких АЛУ, а сигналы G и Р - для организации параллельного переноса в 4т-разрядных АЛУ, построенных на тп 4-разрядных секциях. Выражение (6.55) формально совпадает с первым из соотношений (6.48) для c,+i, а значит, параллельный перенос между 4-разрядными секциями АЛУ выполняется так же, как и между отдельными разрядами 4-разрядного сумматора (рис. 6.100) - с помощью устройства переноса CRU (Carry Unit). При подаче на АЛУ инверсных операндов А" и У функции fi и (fi примут вид: fi = х{у{Е3 V xiyiE2, (fi = х{ V yiEx V у{Е0. На основании (6.43) для прямых переносов cq и с4 и инверсных разрядов суммы s, можно получить: c.+i = 9i V PiCi, ci = д0 V pQc0, С2 = 9\ V V\c\ = 9\ V Р\9о V pipoco, сз = 92 V р2с2 = д2 V р2дх V p2pig0 V Р2Р1Р0С0, С4 = дз V р3#2 V р3Р2#1 V РЗР2Р190 V РзР2Р1Р0С0, G = 9з V Рз92 V p3p2gi V рзР2Р19и, P - P3P2P1P0, c4 = G V P c0, Щ = gi 9 Pi Ф с{, где gt = fnpi = ft = х{у{Ез V х{у{Е2, p, = ftVipt = <p{ = х{ V V j/o- Так как функции получаются заменой в s, переноса с, на с, V М, то = (xiViE* v г,-у,-£2) е (г,- v у& v j/,£0) е (г,- v м). В табл. 6.23 представлены функции, выполняемые АЛУ для прямых X, У и инверсных А", У операндов. Здесь использованы обозначения: О = 0000, 1 = 1111, С0 = 000с0, "V" -поразрядная дизъюнкция, "&" - поразрядная конъюнкция, А" и У - поразрядное инвертирование операндов, "+" - арифметическая сумма. Результат операции в табл. 6.23 указан для функции F = F3F2F1F0 независимо от того, используются ли 0 ... 86 87 88 89 90 91 92 ... 119 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||












