Раздел: Документация
0 ... 89 90 91 92 93 94 95 ... 119 MCI 4530В £3 £3 в - GND.te - Vp,, Рис. 6.125 a) г,- la-
Г
Рис. 6.126 функций: /5 = 1, 14 = 0 =» F = (Л/г V 7i/3 V /2/3) Ф Р - 3-входовой МЭ, с возможностью инвертирования функции выхода F, 15 = 14 = 0 => F = Ji/2/3 Ф i5 - 3-входовой ЛЭ И/И-НЕ, I5 = I4 = 1 => F = (h V /2 V /3) Ф Р - 3-входовой ЛЭ ИЛИ/ИЛИ-НЕ, 1Ь = I4 => F = (Л/2/з V /1/4 V /2/4 V /3/4) Ф Р - 4-входовая пороговая схема с порогом к - 3 и неравными весами входов (вход I4 имеет вес вдвое больший, чем остальные входы) с возможностью инвертирования функции выхода. На мажоритарных элементах можно построить асинхронные потенциальные триггеры, если ввести обратную связь с выхода на один или два входа МЭ, так как это было сделано в § 6.4 при синтезе триггеров на мультиплексорах. На рис. 6.126,а показан асинхронный потенциальный триггер, описываемый функцией переходов г\+ - т. тг т. \i п . 7.1-7- где hhh = SW - сигнал установки триггера в состояние Q = 1, /1/2/3 = Rm - сигнал установки триггера в состояние Q = 0. При одновременном изменении нескольких входных сигналов могут возникнуть состязания (см. fj 2.2), приводящие к неправильному срабатыванию триггера. Полученный Дд/-5д/-триггер отличается от R-S-триггеров, рассмотренных в § 3.3, тем, что условие RmSm - 0 выполняется автоматически при любых значениях входных сигналов /*. На рис. 6.126,5 изображен асинхронный потенциальный Rm~Sm-триггер, описываемый функцией переходов где rir2 = Sm - сигнал установки состояния триггера Q = 1, 71/2 = Rm - сигнал установки состояния Q = 0. Функции возбуждения триггера могут быть найдены методом, изложенным в § 1.6: /2 = Q+QV М<Э+ VQ), /i = Q+Q V h2Q+ \/ hiQ+ \Zh2hiQ. 6.13. Умножители двоичных чисел Производительность ЭВМ в значительной степени определяется временем выполнения операции умножения. Программная реализация в микроЭВМ операции умножения двух операндов X и У с помощью операций сдвига и сложения требует значительного времени. Наибольшее быстродействие достижимо в умножителях, выполненных на основе КС. Простейший способ построения комбинационного умножителя п х m-разрядов следует из алгоритма умножения двоичных чисел: Р = ХхУ = Хх (ym i2m-1 + • • • + ТЛ21 + у02°) = тп - 1ш-1 = £ х х Viv = е Pi, 3=0i=o где X = хп-\ ...xiXq - множимое, У - ym-i ..-У\Уо - множитель, Pj = X X yj2} - частичные произведения. Процесс -умножения при п = тп = 4 поясняется схемой: 272625242322212° - веса разрядов, 110 1 = X = 13ю, 10 11 = У = 11 110 1 = Р0 = 13, + 110 1 = Pi = 26, + 0000 = Р> = 0, + 1 1 0 1 = Р3 = Ю4, 1 0 0 0 1 1 1 1 = Р = 143, P7P6P5P4P3P2PlP0 = Р- Принцип построения комбинационного умножителя 4x4-разряда, изображенного на рис. 6.127, предельно ясен из вышеприведенной схемы умножения.. Матричные умножители и умножители на основе ПЗУ. Пусть заданы п- и m-разрядные целые числа Хп - i„ i .. .xii0, An = «n-i • • .aiao, Ут = Утп-1 • -2/12/0, P>m = Ьт-1 • • - Mo- Максимальные значения этих чисел равны 2п - 1 и 2m - 1. Тогда (Хп X Ут -- Ап ~Г Р>т )тах = = (2П - 1)(2т - 1) + 2" - 1 + 2т - 1 = 2п+т - 1, т. е. при любых значений Хп и Ут произведение ХпхУт предста-вимо не более чем п + т разрядами. Для двухразрядных чисел 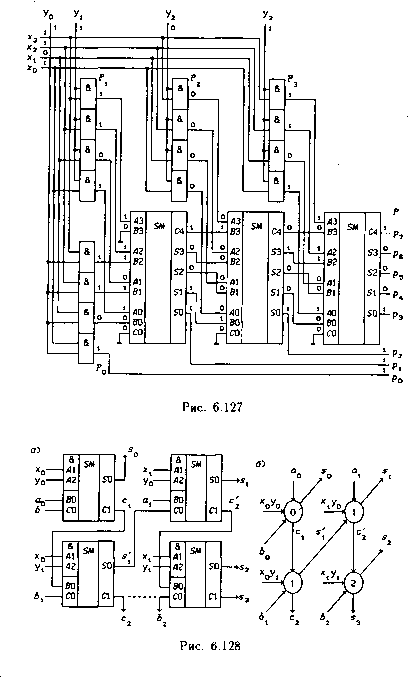 можно записать: Х2 х Y2 + а2 + В2 = xixQ х 2/i2/o + aia0 + ЬХЬ0 = = (1x2х + х02°) х (2/121 + 2/02°) + а1 + а02° + Ь121 + Ь02° = - ii2/i22 + (zxj/o + + ai + bi) • 21 + (xQyQ + a0 + Ьо) • 2°. Эти вычисления могут быть выполнены с помощью четырех одноразрядных комбинационных сумматоров (рис. 6.128,а): Ei = (хоУо + а0 + Ьо) • 2° = сх2х + s02°, выход s0 (вес 2°); Е2 = (хоУ1 + h + ci) • 21 = с222 +выход с2 (вес 22); Ез = (*iSto + 01 + s[) 21 = с222 + г1, выход si (вес 21); Е4 = (xiVi + с2 + сг) • 22 = с323 + 5г22, выходы s2 (вес 22) и s3 = с3 (вес 23). Очевидно, что Х{ xyi = х,&2А:» поэтому арифметическое умножение выполняется ЛЭ И, а сумматоры выполняют функции 50 = Ао © Во © Со, сх = а0в0 v а0с0 V В0С0, где Ло = Л1Л2. На рис. 6.128,6"показано упрощенное условное обозначение такого умножителя двухразрядных чисел (выход с2 не подключен ко входу Ь2 для получения возможности наращивания разрядности умножителя). Сумматоры обозначены кружками, внутри которых указано число г + j, характеризующее вес произведения Х{Ху}, равный 2,+-?. На рис. 6.129 приведен умножитель двух 4-разрядных чисел, построенный на основе умножителей 2-разрядных чисел (входы для подачи произведений Х{ х j/j не показаны). Если положить а, = 0 и bj = О (г = 0,1,2,3, j = 0,1,2,3), то схема будет выполнять функцию Р = рт • • -PiPo = x3...xix0 х 2/3 .. .yi 2/0. Из рис. 6.129 видно, что схема умножителя имеет регулярную структуру и может быть расширена до любых значений п и т. Такие КС называются матричными умножителями. Матричные умножители могут быть построены на одноразрядных сумматорах и с иной структурой межразрядных связей. На рис. 6.130 показаны ИС умножителей MPL (Multiplier): 561ИП5 - матричный умножитель 2x2 разряда, выполненный по структурной схеме, показанной на рис. 6.128,а; 74284- умножитель 4x4 разряда на основе ПЗУ с выходами старших разрядов произведения Р7Р&РЪР4 (е = е\е2 - стробирующий сигнал; при значении е = 0 все выходы принимают значение 0); 74285- умножитель 4x4 разрядов на основе ПЗУ с выходами младших разрядов произведения P3P2P\Pq (е - е\е2 - 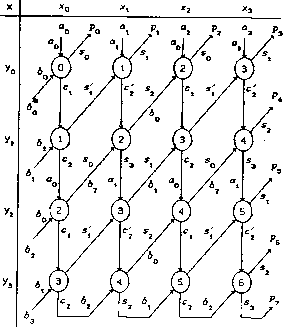 Рис. 6.129 561ИТ5
284 7 4 3 2 1 1Д 13 1 4 285
е - Ш, ie е - 6MD. е - c#d, ie х- & У- 561ИП5 =1 Игл Рис. 6.131 стробирующий сигнал; при значении Е = 0 все выходы принимают значение 0). Все одноразрядные сумматоры умножителя 561ИП5 построены по схеме, изображенной на рис. 6.131: s = х • у ® а ф 6, с = a • Ь V a • (х • у) V Ь • (х у). На рис. 6.132 показала схема матричного умножителя 4x4 разряда, выполненная на ИС 564ИП5 в соответствии со структурой, изображенной на рис. 6.129. Аналогично могут быть построены н матричные умножители nxm, гдеп > 4 и тп > 4. Умножители на основе ПЗУ выполняются записью в них таблицы умножения n-разрядных чисел, что требует объема памяти ПЗУ 2п - 22в бит, 2п входов и 2п выходов. Понятно, что такие умножители могут быть реализованы только для небольшого числа п из-за быстрого увеличения с ростом п необходимого объема памяти, а также увеличения числа выводов ИС. Например, умножитель 8x8 разрядов требует 1 Мбит памяти и имеет 32 вывода для подачи сомножителей и выдачи 16-разрядного произведения. На рис. 6.133,а показан умножитель 4x4 разряда, выполненный на ИС 74284 и 74285, а на рис. 6.133,5- его упрощенное графическое обозначение. Каждая ИС содержит дешифратор адреса, выполненный в виде матрицы 24 строк и 24 столбцов. На адресные входы дешифратора подаются разряды сомножителей А" и У, что обеспечивает выбор одной из ячеек памяти, в которой запрограммировано значение произведения А х Y (или только часть разрядов произведения). На основе ИС 74284 и 74285 можно построить умножители пхтп разрядов при любых значениях пит. Пусть требуется получить умножитель 8x8 разрядов. В этом случае сомножители можно записать в виде X = ХмХь и Y = Уд/Уь , где Хм = х7х6х5х4, XL = 3:3*2*1*0, Ум = У7УвУьУ4, YL = узУзУгУо- Тогда произведение 8x8 разрядов можно представить в виде: Р = X xY = (ХМ24 + XL2°)(YM 24 + yL2°) = = (XMxYM)-2* + (XMxYL)-2* + (XLxYM)-24 + (XLxYL)-2°. Из этого следует, что умножитель 8x8 разрядов должен содержать четыре умножителя 4x4 разряда для вычисления произведений Хь х YL, XL х YM, Хм х YL, Хм х YM 0 ... 89 90 91 92 93 94 95 ... 119 |












