Раздел: Документация
0 ... 90 91 92 93 94 95 96 ... 119 СО Уо-Уэ-
Л Уо-У1- Я61ИПЯ Уэ-
MPL сг Гз ?4 □ у2- Уз- mpz. сг р7 Рис. 6.132 MPL со &£ Hi MPL Рл 2вЗ/2в4 MPL 4x4 хо xi хг хз уо у1 уг уз pi! рг рз Р4 Р5 Р6 4 Р7- и двоичные сумматоры для сложения произведений, получаемых на выходах четырех умножителей 4x4. Структурная схема умножителя 8x8 разрядов, построенная на основе ИС 74284 и 74285, показана на рис. 6.134,а. На выходах умножителей 4x4 разряда указаны веса разрядов 23 полученных произведений. Выходы с одинаковыми весами для сумматоров логически равноценны, поэтому они могут подаваться на любые входы сумматоров, имеющих такой же вес. Из рис. 6.134,а видно, что имеется по три разряда с весами от 24 до 211, а значит, все четыре полученных произведения не могут быть просуммированы одним двоичным многоразрядным сумматором. Для сокращения числа разрядов, имеющих одинаковый вес, до двух, включены 8 одноразрядных сумматоров. Для получения результата 16-разрядного произведения теперь достаточно использовать 12-разрядный сумматор или ALU-12. Рассмотренная схема эквивалентна умножителю 8x8 разрядов, выполненному на ПЗУ (ROM - Read Only Memory - память только для чтения) объемом 1 Мбит с записанной таблицей умножения 8-разрядных чисел (рис. 6.134,6). Быстрые умножители. Пусть требуется вычислить произведение двух целых положительных чисел X = жп г.. .хгх0 и Y = УбУ5У4УзУ2У1У0-Тогда произведение Р = X X Y можно представить в виде 6 Р = X (у626 + уъ2ъ + у424 + уз23 + у222 + у1 + у02°) = £ Pj. 3=0 Величины X • yj 23 = Pj называются частичными произведениями. Число частичных произведений равно числу разрядов множителя Y. Рассмотренный выше матричный умножитель (рис. 6.132) и производит вычисление таких частичных произведений с совмещением операции их суммирования в каждой ступени вычисления Pj. Выражение для Р можно преобразовать к виду: Р = X [(0 + у6 + у5)26 + (-2у5 + У4 + Уз)24 + +(-2у3 + Уг + Уг)22 + (~2yi + Уо + 0)2°] на основании элементарного соотношения yj2> = yj2j+x -2yj2j-\ используемого для нечетных значений j. Все частичные произведения X • (-2i/. Li 4- и, + и,-!) • 23 а) "2- *з-Уэ-
MPL 4x4 РО Р1 Р2 РЗ Р4 Р5 Р6 Р7
MPL 4x4 РО Р1 Р2 РЗ Р4 Р5 Р6 Р7
РО Р1 Р2 РЗ Р4 PS Р6 Р7 MPL 8x8 RDM 1 *5tt SM > 1 -i CO SM SM SM SM SM SM /10 £0 FO At FI /Ш/-12 SI A2 B2 A3 S3 At 54 Д5 S5 /16 86 A7 B7 ДВ BB /19 B9 AiO 810 /111 811 F2 F3 F4 F5 F6 F7 F8 F9 F10 Fll • Po Pi P* Рз P4 Рв Pic hPl2 "Pis Pl4 Pis имеют одинаковую структуру, а их число уменьшилось вдвое по сравнению с числом частичных произведений X • j/j • V, т. е. при использовании рассмотренного преобразования в каждой ступени вычисления частичного произведения производится умножение сразу на два разряда множителя У. Такой метод вычисления произведения называется модифицированным алгоритмом Бута. Легко показать, что алгоритм Бута справедлив и для умножения двоичных чисел, представленных в дополнительном коде, причем произведение выдается также в дополнительном коде. Покажем, что частичные произведения X • (-2 • i/j+i + yj + Vj-i) достаточно просто реализуются с помощью КС. Не теряя общности, можно положить j = 0, тогда функционирование КС будет описываться выражением: X-N = X-(-2yi + y0 + y-i). Так как yj = 0 или 1, то величина в скобках может принимать значения от -2 до +2, т.е. число N = -2, -1,0, + 1,+2. Пусть X N = - 2Х. Это означает, что множимое X следует сдвинуть на один разряд влево, а результат необходимо представить в дополнительном коде для выполнения суммирования частичных произведений. Дополнительный код частичного произведения в этом случае [-2Х]д = 2Х + 1. При этом возникает задача расширения разрядной сетки частичных произведений до разрядной сетки всего произведения Р = X xY, которое имеет большее число разрядов по сравнению с младшим частичным произведением. Пример 1: X = +5, У = +6, Р = X х Y = +30 0.101= [+5]д, {У]д=0110 х 0.110= [+6]д,(10 0) => -2Х 2° = -Л" • 21 1 11.0 110=[-Х-21]д, (011)=> + 2Л-22 = +А-23 + 0.10 1 000= [+Х 23]д, 0.01 1 110= [Р]д. Пример 2: X = 19, У = -27, Р = X х У = -513 0.10011= [+19]Д [У]д=1.0010 1 х 1.00101= [-27]д,( 0 1 0 } => +Х 2° 0 000 00.10011= [+Х-2°]Д,(010 )=> + Х-22 + 0 000.1 0 01100= [+Х-22]Д) (100)=>-X -25 ~*~1.01 1 0 1 00000= [-Х 25]д, 1.0111111111= [Р]д. Таблица 6.27. Быстрый умножитель 4x2 разряда
 Рис. 6.135 Табл. 6.27 задает функционирование 4 X 2-разрядного быстрого умножителя, где [X N]o - обратный код числа X N, X = x3x2x\Xq. Функция D\ введена для расширения разрядной сетки частичных произведений, а функция со предназначена для преобразования обратного кода в дополнительный. Из диаграмм Вейча (рис. 6.135; х» = xr-i), составленным по табл. 6.27, видно, что со = У1У0У-1,(6.60) а функции Dr (г = 0,1,2,3) минимизации не поддаются, т.е. Д. = xrK~i V xrK2 V Xr-iA3 V x"r-iA4 V xrА5 V xrA6, Кг = у\1Уо°У--х-Функции Dr и D\ несложно представить в форме Dr = Хг.гН Vxr !/i2yi Vxr/i3yj Vxrh3yi, r = 0,1,2,3, D4 = x3h{yx V x3h2yi V х3к3уг V x3h3yx,(6.61) где hx = 2/0У-1, h2 = y0y 1? h3 = y0 © y i- По этим функциям может быть построена КС, реализующая быстрый умножитель Л о----„ *± л £л лгрлДо.. На рис. 6.136 показаны ИС: х -1 о Щ 1 2 3 "I 2 555ИП8 531ИК1 261 е - S#D, is -
12 - GND, 24 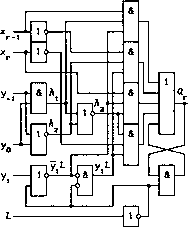 Рис. 6.136 Рис. 6.137 555ИП8 - быстрый умножитель 4x2 разряда, построенный в соответствии с (6.60) и (6.61); 531ИК1 - быстрый умножитель 4x2 разряда с сумматором частичных произведений. Умножитель 555ИП8 содержит пять асинхронных потенциальных /-Х-триггеров для фиксации функций Dr:= DTL V QrL, где г = 0,1,2,3,4. Схема разрядов Dr (г = 0,1,2,3) показана на рис. 6.137. Если L = 1, то осуществляется прямая передача значений Dr на выходы Qr. Фиксация значений Dr в триггерах Qr используется для построения быстрых конвейерных умножителей (см. § 6.14). Таким образом, ИС 555ИП8 может использоваться для проектирования как конвейерных, так и обычных п х m-разрядных быстрых умножителей. На рис. 6.138 показана схема быстрого умножителя 8x4 разряда. Четыре ИС 555ИП8 (L = 1) формируют два частичных произведения с весами разрядов от 2° до 29 и от 22 до 211 (сигналы соо и С02 необходимы для преобразования обратного кода в дополнительный). Константы единица с весами 28, 29 и 211 добавляются для правильного суммирования частичных произведений в дополнительном коде с расширением разрядной сетки. Так как частичные произведения представляются в дополнительном коде, то и сомножители должны подаваться на умножитель в дополнительном коде. Понятно, что произведение Р = X X Y = рц .. .ргро будет также представлено в дополни- 0 ... 90 91 92 93 94 95 96 ... 119 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||












