Раздел: Документация
0 ... 93 94 95 96 97 98 99 ... 119 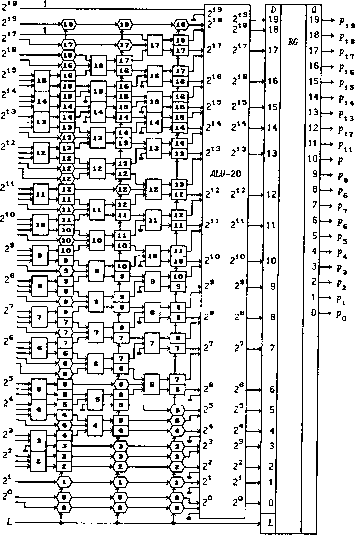 логикой; цифрами внутри перечисленных узлов указаны веса их входных сигналов). Часть схемы на рис. 6.150, построенная на одноразрядных сумматорах, представляет собой дерево Уоллеса, преобразующее 61 разряд четырех частичных произведений в совокупность разрядов, в которой разряды с весами V (j = 0... 19) встречаются не более двух раз. Данная совокупность разрядов может рассматриваться как два 20-разрядных двоичных числа, для суммирования которых необходим 20-разрядный двоичный сумматор или ALU-20. Предпочтительнее использовать быстродействующее ALU-20 с параллельным переносом, так как эта (последняя) ступень конвейера является наименее быстродействующей из-за переносов между 4-разрядными секциями АЛУ или сумматоров. Для реализации дерева Уоллеса требуется 39 одноразрядных сумматоров (20 ИС 555ИМ5), для фиксации результатов преобразований информации в последних четырех ступенях конвейера - 136 D-X-триггеров (17 ИС 555ИР22 или 1533ИРЗЗ). Для увеличения производительности конвейерного умножителя при построении схемы ALU-20 можно использовать ИС 53ШПЗ и 531ИП4. Конвейерные АЦП. На рис. 6.151 показана структурная схема 8-разрядного параллельного аналого-цифрового преобразователя (АЦП) с конвейерной обработкой данных 1107ПВ2. Аналоговое входное напряжение - 2 В < Vj < 0 В преобразуется этим АЦП в 8-разрядное число Q = q7 . QiQo - Схема АЦП содержит 256 аналоговых компараторов С,- (г = 0 ... 255), в которых производится сравнение входного напряжения V/ с опорными напряжениями, формируемыми резистивным делителем из напряжения VJrki = -2 В, подаваемого на выводы 22 и 11 (RV - Reference Voltage - опорное напряжение). Каждый компаратор содержит триггер для реализации первой ступени конвейера. Приоритетный шифратор PRCD 256 х 8, ЛЭ сумма по модулю два и выходной буферный регистр RG составляют вторую ступень конвейера. Сигналы Р2 и Р\ используются для инвертирования выходных сигналов шифратора в соответствии "с табл. 6.32. Ре-, зистор Rcn может подключаться к выводу 11 или 22 для коррекции нелинейности преобразования (CN - Correction Nonlinearity). На рис. 6.152 показаны временные диаграммы работы АЦП. По положительному фронту тактового сигнала Н производится выборка значения аналогового напряжения Vj, в паузе между значениями сигнала Н = 1 производится шифрация выходных сигналов компараторов (преобразование в 8-разрядный двоичный код) и следующим положительным фронтом тактового сигнала осуществляется запись полученной информации в выходной буферный регистр RG. Информация на выходе АЦП появляется с задержкой на два такта относительно входной информации. Благодаря конвейеризации достигнута частота преобразования 20 МГц. 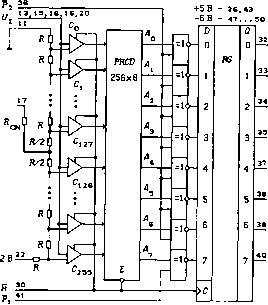 Рис. 6.151 П07ЛВ2 П07ПВ1
-2В- б ~~ХКод *-2ХКод Я-1Х Код Н
Таблица 6.32. Функционирование АЦП 1107ПВ2
Таблица 6.33. Основные параметры АЦП 1107ПВ1 и 1107ПВ2
На рис. 6.153 показаны условные графические обозначения 8-разрядного АЦП 1107ПВ2 и 6-разрядного АЦП 1107ПВ1, который отличается от первого АЦП только числом разрядов. Подробное описание ИС 1107ПВ1 можно найти в [29]. Основные параметры этих АЦП приведены в табл. 6.33. АЦП имеют выводы аналоговой земли r\GND и цифровой земли #GND (GND - Ground - земля). 6.15. Синтез линейных комбинационных схем Для проектирования линейньгх цифровых автоматов над полем GF(q) при q ф 2 необходимо использовать специальный набор базовых ЛЭ, выполняющих операции сложения и умножения по модулю q. Такие ЛЭ являются достаточно сложными устройствами, синтез которых можно выполнить в виде КС на основе двоичных сумматоров и стандартных ЛЭ. Любой автомат над полем GF(q) может быть построен на £)-триггерах и вышеуказанных ЛЭ (никакие другие элементы не требуются). Сумматор по модулю q. На вход сумматора по модулю q могут поступать числа 0 < X < q - 1 и 0 < г < ? - 1. Сумматор должен вычислять сумму Z = (X + Y)q, где число Z равно остатку от деления суммы X + У на число q. Понятно, что для чисел q, X, Y и Z можно использовать двоичное представление, т. е. эти числа можно записать в виде: q = qn qp 9ь X = x„...xp...xi, Y = уп-..ур...у1, Z = zn ... zp ... zt, где qp, xp, yp и zp - двоичные разряды соответствующих чисел. Требуется синтезировать сумматор по модулю q при любом значении п. Традиционные методы синтеза (таблицы истинности, диаграммы Вейча) не могут быть использованы для логического проектирования сумматоров по модулю q, так как по условию задачи число двоичных разрядов не задано. В данном случае следует воспользоваться арифметическими свойствами входных и выходных переменных, а в качестве основных элементов - двоичными 4-разрядными сумматорами 555ИМ6 и 561ИМ1. Рассмотрим двоичную сумму S = (X+Y)+(2n-q),(6.63) где S = sn+isn ... sp ... si, а вес двоичного разряда s„+i равен 2" (отметим, что сумма весов всех остальных разрядов равна 2" - 1). Очевидно, что сумма S может принимать значения: S < 2" и S > 2" в зависимости от значений чисел X и У (однако, следует иметь в виду, что при любых значениях чисел X и У сумма S < 2"+1). Если сумма S < 2", то Sn+i = 0, и из соотношения (6.63) следует, что X +Y < q, а значит, Z = X+Y = S-2" +q = (S + q), где символ (А) означает исключение у величины А = a„+ia„...ai старшего разряда an+i, т. е. (А) = а„ ... а\. Если же сумма S > 2", то s„+1 = 1, и из соотношения (6.63) следует, что X + Y > q, а. значит, Z = X+Y-q = S-2n = (S). Таким образом, имеет место соотношение: f (S + q), если s„+i = О, Z = (X + Y)q = {4hn+16.64 ( (5), если sn+i = 1. На основании соотношения (6.64) может быть построена схема сумматора по модулю q, где q - любое простое число. На рис. 6.154 показана схема сумматора для случаев, когда число q можно представить не более чем четырьмя разрядами (q = 3, 5, 7,11 и 13). Двоичный сумматор D1 производит вычисление суммы чисел X = Х4Х3Х2Х1 и У = УаУзУъУх, двоичный сумматор D2 вычисляет сумму S, определяемую соотношением (6.63), поскольку 24 - q = <?4<?з92<71 + 0001 - дополнение числа q до числа 24. Разряд s„+i = S5 суммы (6.63) формируется с помощью ЛЭ ИЛИ. Если S5 = 0, то ЛЭ ИЛИ-НЕ выдают число q = 94939291, поступающее на входы двоичного сумматора £>3, который и вычисляет сумму Z - (X + Y)q. Если же s5 - 1, то ЛЭ Уз" *з" У2-*2" У," *1" з-
1-
-ГП- <- к 1 ф- I- 16- п
4 2 Рис. 6.154 ИЛИ-НЕ выдают число 0 = 0000. Таким же способом могут быть построены сумматоры по модулю q для любого q = qn...qi, где п > 4. В структурных схемах будем использовать для сумматоров по модулю q условное обозначение, показанное на рис. 6.155,а. Если q = 2" - 1 (при п = 2,3,5,7,13,17,19,31 числа q - простые), то схема сумматора по модулю q упрощается, так как 2" -q = 1 и сумма (6.63) вычисляется с помощью одного двоичного сумматора (число 1 подается на вход сумматора Dl, а сумматор D2 и ЛЭ ИЛИ исключаются). При q = const схема сумматора по модулю q может быть упрощена за счет исключения ЛЭ ИЛИ-НЕ. В этом случае следует получить сигнал s„+i и подать его на входы двоичного сумматора 1?3, соответствующие числу q. На рис. 6.156 показана схема сумматора по модулю 7 (7 = 23 - 1), выполненная на основе 4-разрядных двоичных сумматоров (здесь достаточно было бы использовать 3-разрядные двоичные сумматоры). Умножитель по модулю q. Один из сомножителей, например У, можно представить в виде: p=i где У = уп ... ур ... у\ - двоичное число. Тогда для произведения чисел X • У имеет место соотношение: п X Y = урХ 2Г-\ Р=1 0 ... 93 94 95 96 97 98 99 ... 119 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||












