Раздел: Документация
0 ... 88 89 90 91 92 93 94 ... 119 550 Глава 6. Коммутаторы и арифметические устройства со 0W-A о < в Р OW-A <с с I О 4 в Р AUJ-A С < О 4 С Р rV0c OW-A G Р OW-XB СРМ AW-X6 =1б G Р 0W-XB *Ас с 0 18 G Р 0W-XB о =ie G Р 0W-XB 1 G Р 4Лс с г О 18 ДИ/-64 СИ/ D Рис. 6.118 Таблица 6.26. Быстродействие АЛУ
.11. Арифметическо-логические устройства 551 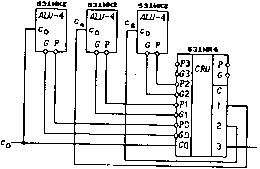 С,2 Рис. 6.119 X1 Y X* Y F1
Рис. 6.120 "ASBBIA -ASBBIA -ASBBIA -ASBBIA -ASBBIA AS881A -ASBBIA ASBeiA AW aw aw iff
aw О 4 . „- - с "---- о-оо-о---6-6 б □ Vo <?im 8 СгРг G3P3C G,Pt G3P, =« Сере Сэг Рис. 6.121 ASBeiA -AS881A ASfA -AS881A AS8B1A -AS8S1A S681A as881a 0W G P AW G P aw G p aw co G P\ + + + +p r. i i i x in i j. i : : . ?\ ! e 7 7 <? p С P co G P ди/ co G PI t f 1 t tp. saf t 1 t tp3 c,+ t ; t tp, v t : [ •i i f i 4 > * Ir-"tit tf U ▼ 1 olII : f ; ! * + I ! s s! ! + с . Vo V, =e G2P2 G3P3crS ё4Р4 С5Р3=24 c6Pe ё7Р7 =э ASB82A с16 = G*3 V P3G2 V P3P2G1 V P3P2P1G0 V P3P2PiP0c0, с24 = G5 V Р5С4 VV P5P4P3G2 V PbP4P3P2Gx V ЧРьРАР3Р2РхСо V P5P4P3P2PiP0c0, c32 = G7 V P7G6 V PtGs V P7P6P5G4 V P7P6P5P4G3 V VP7P6P5P4P3G2 V Р7РбР5Р4РзР2С \ZP7P6P5P4P3P2P1G0 V P7P6P5P4P3P2PiPqc0. На рис. 6.121 представлена структурная схема Л/,£/-32 с параллельно-последовательно-параллельным включением восьми AZ£/-4. Последовательно переносы проходят только через два AZf/-4, т.е. четыре пары AZ{/-4 включены параллельно-последовательно и представляют собой ALU-8, а полученные четыре ALU-8 включены параллельно. Быстродействие таких АЛУ приближается к быстродействию параллельных АЛУ. Устройства переноса 4Л5882А можно использовать и для построения ALU-64 с параллельным переносом (рис. 6.122). Последовательные переносы, имеющиеся в предыдущей схеме, заменены на параллельные с помощью второго устройства переноса 74Л5882Л. Устройство переноса 74AS282 предназначено для построения синхронных параллельно-последовательных АЛУ, выполняющих арифметические операции с двойной точностью. Принцип работы таких АЛУ основан на том, что 2 х 4т-разрядные числа обрабатываются в АЛУ-4ш за два такта как 4т-разрядные числа. Экономия аппаратных затрат получается за счет увеличения времени выполнения арифметических операций. Устройство переноса 74Л5282 описывается функциями: с4 = Go V P0CY, c, = G,V PjGo V PPoCY, C12 = G2 V P2Gi V P2PiG0 V P2PiP0CY, G = G3 V P3G2 V P3P2G1 V PzP2PxGo, P = P3P2P1P0, где перенос CY = c00SiSo Vc0oSiSo Vc0iSiSo VcoiSiSq. Сигналами Si и So производится мультиплексирование источника переноса с указанием его активного уровня для работы с прямыми или инверсными операндами (Si - селекция переноса соо илис01, So - задание активного уровня переносов c0j или с0;, j = 0 и 1). На рис. 6.123 показана структурная схема параллельно-последовательного ALU-32 при работе с инверсными операндами - арифметические операции над 64-разрядными числами X = хез х1хо и Y = j/63 • • -УгУо выполняются за два такта. При выполнении операции сложения в первом такте вычисляется сумма 131 • • XiXq + J/31 .. .yij/o + с0 и перенос С32, который запоминается в синхронном £>-триггере, а во втором такте - сумма х63 • • • г33*32 + УбЗ • • • 1/ЗЗУ32 + С32 AS881A ASSaiA AS881A ASBBIA ASSSIA AS881A ASBB1A AS881A С
ALU G Р Ж ALU G Р ж ALU G Р si so ALU ca в Р Ж ALU °0 G Р Ж ALU G Р ж ALU С0СЛ G Р Ж
с32 Рис. 6.123 к перенос ce4. Мультиплексирование 32-разрядных чисел и источника переноса производится одновременно. Рассмотренную схему можно использовать и для сложения k х 32-разрядных чисел за ifc тактов. Соотношения (6.58) можно представить в более общем виде тп - 1 т -1т -1т-1 ст = V 9i П pi V с° П Р и П pi = 1 1=0 j =i+lj=0j" =i+l если i+1 > га-1 (при использовании 4-разрядных секций АЛУ выходные переносы с,- = С4т). Эти выражения при m = 1,2,... ,8 описывают функционирование ИС 589ИК03 (рис. 6.116). Сигнал ЕС» = 0 переводит выход переноса С» в -состояние. С помощью одной ИС 589ИК03 в соответствии с рис. 6.117 можно построить ALf/-32 на восьми ALU-4 1533ИПЗ. Сигнал Се устройства переноса 589ИК03 будет являться выходным переносом С32 ALU-Z2 с прямыми операндами. 6.12. Пороговые схемы и мажоритарные элементы Пороговой схемой к из п называется АС, имеющая п входов 1ш один выход и реализующая функцию f(v\= I * 1X3111 Хр - * JK 1 0, если 2>р < к, где v - (хп, ,хр,... ,xi), 1 < к < п (суммирование осуществляется по всем значениям р = 1,2,..., п). При значении к = 1 iпороговая схема вырождается в n-входовой ЛЭ ИЛИ, а при значении к = п - в о-входовой ЛЭ И. Пороговые схемы используются в обнаружителях сигналов, работающих по принципу к из п (п - число выборочных значений случайного процесса, к - число выборочных значений, превысивших заданный порог, т. е. анализируемые случайные величины принимают только два значения - 0 или 1). В этом случае символы 0 и 1 являются числами 0 и 1, поэтому такие КС могут быть реализованы с помощью двоичных сумматоров. Так как все входные переменные имеют одинаковый вес - 1, то для их сложения с целью последующего сравнения с порогом к требуются одноразрядные двоичные сумматоры. При реализации пороговых схем в МНФ в базисе И-НЕ потребовалось бы в первом ярусе (£) ЛЭ И-НЕ, так как наименьшее число сочетаний входных сигналов, сумма которых достигает или превышает порог к, равно (£). Второй ярус состоит из одного ЛЭ И-НЕ с числом входов (£) = п\/к\(п - к)\. Пусть требуется синтезировать пороговую схему, задаваемую параметрами п = 9 и к = 6. При реализации данной пороговой схемы в МНФ в базисе И-НЕ потребовалось бы (§) + 1 = 9!/б!3! 4- 1 = 85 ЛЭ И-НЕ. Такой способ реализации неудовлетворителен. На рис. 6.124,а изображена эта же пороговая схема, реализованная на двоичных сумматорах 555ИМ5, 155ИМ2 и 555ИМ6. Все входные сигналы хр имеют вес 2° = 1, поэтому они подаются на входы сумматоров, имеющих вес 1. Выходные сигналы сумматоров подключаются ко входам других сумматоров с учетом их весов 2. На вход 4-разрядного сумматора с весом 2 подана константа 1 для смещения порога к до уровня 23 = 8. Тогда ПРИ 12p=i хр > 6 сигнал, равный 1, будет появляться на выходе 4-разрядного сумматора с весом 8. На рис. 6.124,а символами О и 1 показано прохождение некоторой комбинации значений сигналов Хр через все сумматоры. Рассмотренная пороговая схема может быть построена и на трех 4-разрядных сумматорах 555ИМ6, один из которых включается по схеме двух одноразрядных сумматоров (см. рис. 6.103,а). Мажоритарным элементом (МЭ) называется пороговая схема с нечетным числом входов п, выходной сигнал которой равен 1 только при поступлении на ее входы не менее к = (п + 1)/2 входных сигналов хр, равных 1. Для реализации 13-входового МЭ в МНФ в базисе И-НЕ потребовалось бы (13!/7!б!)+1 = 1717 ЛЭ И-НЕ, один из которых должен иметь 1716 входов. На рис. 6.124,5приведена схема 13-входового МЭ, выполненная на четырех одноразрядных (Dl и D2), двух 2-разрядных (D3 и D4) и одном 4-разрядном (-D5) двоичных сумматорах. На один из входов 4-разрядного сумматора D5, имеющих вес, равный 1, подана константа 1. Тем самым порог к - 7 смещается со
*1 - «9 -
-/Cv) Рис. 6.124 до значения к = 8. Выходной сигнал с весом 8 сумматора D5 будет равен 1, если 7 или большее число входных сигналов хр примут значение 1. В интегральном исполнении выпускаются мажоритарные элементы (Majority Logic Gate), имеющие 3 (533ЛПЗ и 561ЛП13) и 5 (МС14530.В) входов. Функция, выполняемая 3-входовым МЭ, совпадает с функцией переноса одноразрядного сумматора: / = Х1Х2 V Х1Х3 V 123) где хр - входные сигналы. Синтез МЭ, имеющих 5, 7 и 9 входов, на 3-входовых МЭ был*рассмотрен в § 1.13, а функция, выполняемая 5-входовым МЭ, представлена в .табл. 1.6. Функционирование 5-входового МЭ МС145305 (рис. 6.125) описывается выражением: F = (IJ2I3 V /1/2/4 V /1/2/5 V IJ3I4 V /1/3/5V v/i/4/5 v /2/3/4 v /2/3/5 v /2/4/5 v /3/4/5) е р, (6-59) где Р (Polarity) - сигнал инвертирования функции выхода МЭ. Из соотношения (6.59) при подстановке определенных значений некоторых сигналов следует, что 5-входовой МЭ может использоваться для выполнения различных переключательных 0 ... 88 89 90 91 92 93 94 ... 119 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||












