Раздел: Документация
0 ... 62 63 64 65 66 67 68 ... 82 Если воспользоваться для построения логической цепи элементами НЕ—И, то имеет смысл далее преобразовать функцию к виду Из последнего выражения видно, что для построения пороговой ячейки в данном случае потребуется три двухвходовых и один трехвходовый элемент НЕ—И. Схема синтезированной логической цепи приведена на рис. 11-1. Условные обозначения логических ячеек здесь и далее даны в соответствии с ГОСТ 2.743—72. Логическая ячейка по этому ГОСТ обозначается в виде прямоугольника, входы которой показываются слева, а выходы — справа. Инверсные входы и выходы обозначаются кружками. Внутри прямоугольника помещается информация о функции, выполняемой данным логическим элементом. 11-3. Примерытипичных комбинационных цепей В настоящем параграфе будут рассмотрены следующие примеры типичных комбинационных логических цепей: схемы интерфейса, мультиплексоры, сумматоры. Схемы интерфейса. Рис. 11-2, а и б показывает схемы ИС серии К559, с помощью которых можно организовывать обмен логической информацией а)5)+Е R1 RZ +£ 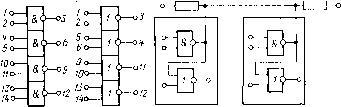 Рис. 11-2. Схемы интерфейса серии К559 (а, б) и вариант их применения (в) между различными измерительными или вычислительными устройствами. Схема передатчика К559ИП1 (рис. 11-2, а) содержит четыре ячейки И—НЕ. Выходные транзисторы этих ячеек включены по схеме с общим эмиттером, но коллекторные резисторы в этих каскадах отсутствуют. Благодаря этому появляется возможность объединять выходы нескольких ячеек И—НЕ, образуя тем самым ячейку И—ИЛИ—НЕ. При этом необходимо дополнить ячейку недостающим коллекторным резистором, сопротивление которого выбирается из условия согласования выходного сопротивления передатчика с волновым сопротивлением линии связи. Схема приемника (рис. 11-2, б) имеет большое входное сопротивление, что позволяет подключать к одной магистрали до 20 пар приемников-передатчиков. Схема устройства обмена информацией, построенного на основе ИС серии К559 для двух объектов, показана на рис. 11-2, в. Резисторы R1 и R2 на этой схеме обеспечивают согласование сопротивлений на обоих концах линии. Как видим, одна н та же магистраль здесь используется для передачи информации в обоих направлениях. Мультиплексор — это коммутатор логических сигналов, он обеспечивает передачу на выход любого из нескольких входных сигналов. На рис. 11-3, а показана схема логического коммутатора К155КП5. Этот коммутатор имеет 8 сигнальных входов В0—В-,, один выход F и три управляющих входа А0—Аг. Сигнал на выходе F равен инверсии сигнала па том входе, номер которого соответствует коду, задаваемому на управляющих входах. В частности, если к управляющим входам Л2, Ai, А0 приложены сигналы 001, то выходной сигнал будет равен инверсии сигнала на входе В\. Строится мультиплексор па основе сочетания логических ячеек И, ИЛИ, НЕ так, как это показано на рис. 11-3,6. а) 5с he 5с 2с 1С IS с 12° 11 с tOo So
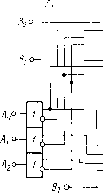
Рис. 11-3. Логический коммутатор К155КП5 (а) и принцип его построения (б) Па основе этого рисунка нетрудно записать логическую функцию, реализуемую мультиплексором, F = АъА1А2,В0 + АъАгАчВ + ААгАфт Сумматор — это логическая цепь, вырабатывающая сигналы суммы (S) и переноса (Р) при сложении двух двоичных чисел. Одноразрядный сумматор должен иметь три входа — два входа слагаемых и вход переноса — с сумматора соседнего младшего разряда. На рнс. 11-4, а показана схема одноразрядного сумматора, положенного в основу ИС типов К155ИМ1, К155ИМ2, К455ИМЗ. Входы слагаемых на этом рисунке обозначены буквами Л и В, а С — это вход переноса. Как следует из рис. 11-4, а, логические функции, реализуемые этим сумматором, описываются следующими равенствами: Р = АВ + АС + ВС, S = AP + ABC-\-BP + CP. (11-4) Таким образом, равный единице сигнал переноса Р появляется тогда, когда хотя бы два из трех входных сигналов (А, В, С) равны единице. Сигнал суммы 5 равен единице в случае, если только один из входных сигналов равен единице и отсутствует перенос или все три входных сигнала равны единице. Нетрудно убедиться, что одноразрядный сумматор может быть построен также на основе реализации следующих соотношений: Р = АВ + АС + ВС;S = АР + А В С+ BP + СР. (11-5) Прн суммировании многоразрядных двоичных чисел сумматоры можно соединять последовательно так, как показано на рис. 11-4, б. На этом рисунке представлена схема суммирования двух трехразрядных двоичных чисел a3a2ai и ЬФФ\. Как видим, вход переноса (С) сумматора младшего разряда заземлен, что соответствует подаче сигнала логического нуля. Поскольку сумматор рис. 11-4, а вырабатывает инверсный сигнал переноса, то суммируемые сигналы второго разряда чисел (а2 и 62) подаются на инверсные входы сумматора второго разряда (эти входы на рис. 11-4, а не показаны). При этом реализуются функции (11-5). Если требуется получить разность двух двоичных чисел, то производят суммирование кода одного числа с дополнительным кодом другого. Дополни- а) А о- 5°-6) S -о S о а, ?а2 Л
S, ? a j SM 6ъ? SM S3 —о Рис. 11-4. Принцип построения сумматора К155ИМ1 (а) и его применение при суммировании многоразрядных двоичных чисел (б) тельный код я-разрядного двоичного числа — это код, дополняющий данный до получения числа, содержащего нули во всех я разрядах и единицу в очередном старшем, (я+1)-м, разряде. Например, дополнительный код числа 101 (старший разряд слева)—это код ОН, потому что он дополняет исходное число 101 до числа 1000; действительно, 101+011 = 1000. Дополнительный код числа легко найти путем добавления единицы младшего разряда к обратному коду. При этом обратный код (инверсный) — это код, получаемый инвертированием значений всех разрядов исходного кода. Обратный код числа 101 равен 010. Добавляя единицу младшего разряда, получаем дополнительный код: 010+001 = 011. Таким образом, если из двоичного числа a3a2ai требуется вычесть двоичное число ЬгЬф\, то разность находится как сумма аза2а1 + &з&2&1 + 001. Входящая в эту сумму единица младшего разряда (001) учитывает различие дополнительного и обратного кодов числа 636261. В сумматоре добавление этой единицы реализуется путем подачн постоянного сигнала «единица» на вход переноса самого младшего разряда. Вычитание чисел удобно производить с помощью сумматоров, имеющих как прямые, так и инверсные входы слагаемых. 0 ... 62 63 64 65 66 67 68 ... 82 |












