Раздел: Документация
0 1 2 3 4 ... 27 Значения £/, и Л нетрудно установить, зная определяемые техзаданием номиналы выходных величин, электрическую схему, в которой работают проектируемые трансформатор или ФМУ, и нестабильность входного напряжения. В [1, 4, 5]-чаще пользуются мощностью нагрузки (номинальной или средневзвешенной). Считаем, что к этой мощности можно перейти, пользуясь формулой Рп=Р ■ КР,(1.2) где Кр = costp • х • г).(1.3) Рн — выходная мощность одной фазы; ф — угол сдвига переменного тока на входе по отношению к входному напряжению; я —коэффициент искажения переменного тока на входе"; г) — коэффициент полезного действия на пути энергии от сети к нагрузке. Для номинального, то есть расчетного, режима значения ф, а и г) задаются в техзадании или могут быть рассчитаны. Поэтому проблемы перейти от Р к Ря не существует. Удобно при проектировании и оптимизации ферромагнитных устройств пользоваться величинами Р, U\, /ь определяющими электромагнитные режимы питающей сети и ФМУ в целом. Это особенно важно, когда частота или число фаз от входа к выходу меняются. Связать входную мощность с другими параметрами и величинами нетрудно через типовые выражения для напряжения и тока [1] £/1 = 4/Сф№1/1Я5с/сзс[В];(1.4) Л = S0K • K0Kn0j/Wu(1.5) ■где Кф—коэффициент формы входного фазного напряжения (для синусоиды Кф = 1,11); —частота напряжения питающей сети по первой гармонике, Гц; Wt — число витков обмотки, включаемой на входное напряжение IV, Sc — поперечное сечение магнитопровода, м2, на котором помещена обмотка Wj (подмагничиваемые участки вычитаются); кзс — коэффициент заполнения сердечника магнитным материалом (данные см. в табл. 3.5); В — максимальная рабочая индукция, Тл, по переменной составляющей; S0K — сечение, м2, окна, в ког тором находится обмотка Wt; п0 — часть площади окна, занимаемая обмоткой Wi).kok — коэффициент заполнения окна обмоточным материалом, о нем сказано в 3.3.2; / — усредненная плотность тока для обмоток, А/м2. Решая совместно (1.1), (1.4), (1.5), получим Р = 4Кф»оК31;Кпк5ок5оВ//1.(1:6) Выражение (1.6) широко употребляется в технической литературе при тех или иных модификациях. Однако в нем не отражена доказанная в работе [2] важная роль соотношения Ks = S0JSC, определяющего геометрическую оптимизацию в целом. Преобразуем выражение (1.6) с учетом показателя величины относительно сечения окна Ks = S0K/Sc(1.7) и параметров относительных значений индукции и частоты B* = BjB0, /,, = /,//,0,(1-.8) где В0 и fio—-базовые значения индукции и частоты, при которых выбираются удельные потери в стали рсо. С учетом (1.7) и (Г.8) выражение (1.6) получит вид P = MpKJ-Bttfl,S\[BA]l(1.9) гдеМР - 4Кф/г0КоКк3сВо/ю .(1.10) Решая (1.9) относительно Sc, получаем одну из центральных для оптимального проектирования ФМУ формул базисного сечения магнитопровода Mp-KsiB.Ju (1.11) Выражения (1.10) и (1.11) нами выделены, так как являются важными для решения вопросов оптимального проектирования ФМУ, что будет очевидным из последующих разделов книги. 1.2. Показатели потерь и теплового режима Потери мощности ФМУ определяют температуру его натрева, поэтому существенно влияют на расчетные параметры. Ограничение потерь мощности за счет соответствующего выбора определяющих эти потери пара- метров и величин всегда свойственно СВЧ ФМУ. Связь между потерями и влияющими на них величинами в технической литературе установлена и доказана [1, 5, 11, 15 и др.]. Выражения для этой связи имеют вид APc = pcfiJ-//.Kcgcc;(1Л2) АРК = PkKokVk/2;(1.13) др = АРС +ДРК = АРК(1+v);(1.14) v = APc/APK,(1.15) где рс — удельные потери в сердечниках магнитопрово-да, Вт/кг, при базовых значениях индукции В0 и частоты /ю (см. раздел 3.3.1); уь у — степенные показатели, установленные опытно; рекомендуется [1] брать yi = = 2, у = 1,5; у СВЧ ФМУ величину у следует выбирать более точно в зависимости от применяемого материала для магнитопроводов и базовой частоты. fi0 (см., например, данные табл. 3. 4); Vc—объем магнитопровода, м2; gc — удельный вес материала магнитопровода, кг/м2; Ук — условный объем катушки; рк — удельное сопротивление, обмоток, Ом • м, с учетом окружающей температуры и частоты протекающего тока; АРС и АРК — потери .активной мощности в сердечниках и катушках; АР —полные потери активной мощности; v —коэффициент отношения потерь активной мощности в катушках к потерям в магнитопроводе. Отметим, что если индукция в сердечниках или ток в катушках несинусоидальны, то. значения АРС и АРК необходимо определять как среднеквадратичные для основных гармоник при соответствующих им частотах Рсо и рк. Для случаев сильно выраженных первых гармоник этого можно не делать. Определение "температуры перегрева ферромагнитных устройств и составляющих их элементов является самостоятельной и весьма сложной задачей, которая в настоящее время успешно решена [1 и др.]. Однако пользоваться известными методами теплового расчета ФМУ целесообразно после определения всех основных параметров этих устройств, то есть на этапе проверочных расчетов. В процессе анализа и синтеза, когда ведется поиск множества величин и параметров (электромагнитных, физических и" геометрических), наиболее полно удовлетворяющих по совокупности своих значений минимуму требуемого удельно-экономического показателя, 8 всегда Желательно применять простейшие тепловые критерии, которые без заметного ущерба для точности решали бы поставленную задачу как можно проще. Нами принимается, что оптимизация ФМУ при заданных температурах перегрева катушек и магнитопроводов обеспечивается с достаточной . простотой и точностью, если пользоваться рекомендованными в [1] обобщенными коэффициентами теплоотдачи сердечников ас и катушек ак. В физическом смысле эти коэффициенты являются отвлеченными величинами и показывают (для конкретных условий охлаждения, материалов и поверхностей), какая активная мощность затрачивается для нагрева единичной площади поверхности на один градус по Цельсию. Значения ас и ак могут быть рассчитаны и определены опытно. Для усредненных расчетов при естественном охлаждении рекомендуется [1] принимать ос = Ок = 10 Вт/м2 • град. Увеличение значений этих коэффициентов зависит от ряда факторов: пропитки, улучшения охлаждения за счет крепления ФМУ к шасси (для ас), дополнительного обдува и т. д. Более подробно о влиянии различных факторов на величины ос, Стк сказано в разд. 3.3.3. В целом значения ос и ак можно установить предварительно, то есть до оптимизации параметров ФМУ, и считать эти коэффициенты в дальнейшем известными параметрами. Для силовых высокочастотных ФМУ характерны два типовых случая теплоотдачи в окружающую среду: а) магнитопроводы и катушки охлаждаются независимо, то есть они теплоизолированы или разделены охлаждающими каналами; б)..тепло магнитопроводов частично или полностью (тороидальные устройства) передается через поверхность катушек. Известные случаи для низкочастотных ФМУ, когда тепло катушек частично отводится через сердечники, практически- не наблюдаются у СВЧ ФМУ. Перегрев сердечников и катушек при независимом охлаждении описывается согласно [1] выражениями: тс = АРс/осПс;(1.16 а) тк = АРк/сХкПк,(.1.16 6) где тс — температура перегрева над температурой окружающей среды для сердечников, град;ттк — то же для катушки; Пс, Пк — поверхности охлаждения магнито-проводов и катушек соответственно, м2. Выражения для Пс и Пк приведены в разд. 1.3. Если теплообмен между магнитопроводом и обмотками существует, то для теплового баланса рекомендуется [1] другое выражение АРК + ДРС = окткПк + а£тсПс = отПкБ,(1.17) где р = Пс/П„.(1.17 6) Здесь а является обобщенным коэффициентом теплоотдачи, одинаковым для катушек и сердечников, у которых невозможен также разный перегрев, то есть 0"к = Ос = о, тк = тс = т. Формула (1.17 а) для Б эмпирическая, но достаточно точная. Для каждой из-составляющих потерь мощности в выражении (1.17) можно записать АРк = ат„ПкБ„;(1.18а) ДРС = отгсПсБс,(1.18 6) гдеБк-Б/1+v;(1.18в) Bc = vB/p(l+v) = BKv/B.(1.18г) Выражения (1.18 а), (1.186) по отношению к (1.16 а), (1.16 6) являются более общими. При независимом охлаждении катушек и магнитопровода в них следует принимать БК = БС=1. Эти выражения играют важную роль в определении величин, требующих ограничения по допустимому перегреву. 1.3. Математическое отражение геометрических показателей Геометрические показатели присутствуют практически во всех расчетных уравнениях ФМУ, причем линейные размеры и геометрия в целом этих устройств ре-щающим образом влияют на их удельно-экономические показатели. Особенно это свойственно СВЧ ФМУ, требующим развитых поверхностей для охлаждения. Ма- тематические выражения объемов сердечников и катушек, поверхностей их охлаждения, средних периметров магнитопроводов и катушек через четыре основных линейных размера магнитопровода — высоту h и ширину с окна, ширину а и толщину b магнитопровода (рис. 1.1) Дают уравнения, определяющие оптимизацию ФМУ в Целом. В отечественной литературе установлены единые обозначения линейных размеров магнитопроводов ФМУ, показанные на рис. 1.1. Все остальные размеры образуются из этих базовых; например, высота и толщина катушек берутся как часть высоты и ширины окна, в котором расположены катушки. Более того, все линейные размеры ФМУ обычно рассматриваются как безразмерные в значениях относительно ширины основного магнитопровода х = с/а, y — b/a, z = h/a.(1-19) К сожалению, исследователями не предложена единая форма уравнений для геометрических показателей ФМУ и приходится записывать их для каждой конструкции, что неудобно для многих вопросов сравнительного анализа. В данной работе для геометрии ФМУ будет использоваться следующая обобщенная система выражений: = SCLC; VK = S0KLK\ Sc = ab\ S0K = he; LK = г (ma -f- nb -f- qc); Lc = r (ma + qc + ph); Пк = лк?А(Л + с); Если за базисную величину для линейных размеров принять сечение основного сердечника магнитопровода $c — ab (на этом сердечнике находится первичная обмотка) и считать, что f-K = /<„ h = KHVse, c = kcVsc, b = KbVsc, a = VSjKb,(1.21) то с учетом (1.21) выражения в (1.20) преобразуются к виду 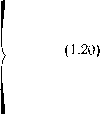 0 1 2 3 4 ... 27 |












