Раздел: Документация
0 1 2 3 4 5 ... 27 с 1-е, 1,5 Пс = ScNJc] Пк = SCNJK, (1.22) (1.23) (1.24) (1.25) r \ \ j V j я с a. с л С 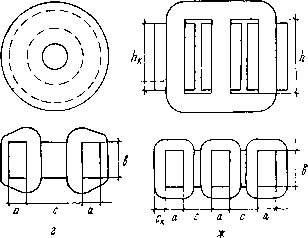 Рис, 1,1. Типовые конструкции ФМУ (начало) где h k а а Q а 3 па dа dа па б a п п □ п ак с А  t ЗС1-5 1ГсТ1Г£сТ е TV ТУ-—-V IP V ч я ■ с a S Рнсг, 1.1. Типовые конструкции ФМУ (окончание) /с = г (т1Кь + ЧКС + pKh); /„ = r{mlKb + nKb + qK0); Nc = 2(l/Kb + паКь/пм)пм; (1.26) (1.27) (1.28) 13 лГ„ = Лкфк(Ял + Яс);(1.29) Ks = hc/ab = KcKh = xz/y.(1.30) В системах (1.20) — (1.30) приняты обозначения: Lc — усредненная протяженность магнитопровода при сечении Sc (средняя силовая линия); LK — средняя длина витков катушек; /с, /к— относительные значения LG и LK; Nc, NK — относительные безразмерные значения величин Пс, Пк; «к — число катушек на фазу; <рк — коэффициент эффективности теплоотвода от катушек. Параметр cpK имеет значения: 1—когда тепло отводится только от наружных поверхностей катушек (см. рис. \Л, а, в, ж), и 2 — когда катушка охлаждается со всех сторон (см. рис. 1.1, д, е). Вводом дополнительных каналов охлаждения значение фк можно увеличивать в я>1 раз. Коэффициенты па и я1Ч также имеют дискретные значения: па — показывает, во сколько раз ширина магнитопровода внутри катушки больше наружной его части. Например, для конструкций на рис. 1.1, а, д, е па = 2, для остальных конструкций на рис. 1.1 па = 1; пм — число частей магнитопровода внутри катушки, разделенное на па (для конструкций на рис. 1.1, <Э, е ям = 5). Безразмерные коэффициенты г, г, m, т, q, q, п, р назовем конструктивными, так как значения их зависят от конструктивного исполнения ФМУ. Для типовых конструкций ФМУ с ленточными магнптопроводами на рис. 1.1 значения конструктивных коэффициентов геометрии приведены в табл. 1.1. Установить значения этих коэффициентов для каждой из конструкций ФМУ нетрудно. Следует записать конкретные выражения для объемов магнитопровода и катушек, затем сопоставить их с обобщенными формулами из системы (1.20) VK = сп ■ r(ma-\-nb + qc);(1.31) Ve.= abr (ma + qc\-ph).(1.32) Например, для броневого ФМУ на рис. 1.1, в будем иметь VH = hKcK (2а + 2Ь + 2*Ск 2 = he ■ nh-пс2 (а + b + 2*/гсс/2),(1.33) где nh = hK/h, /гс = ск/с;(1.34) Ve = у Ьi2h + 2с + 2u j j-2 = ab2 fj a + c + h.(1.35) Сопоставляя (1.31) и (1.33), (1.32) и (1.35), получаем: г —2яля0, т=\, я=1, q — яяс/2, г= 2, т = я/4, q=l, р= 1. При полном заполнении окна пн = 1, пс = 1, что бывает редко. Как правило, СВЧ ФМУ имеют для лучшего охлаждения неполное заполнение окна магнитопровода катушки, при этом ял~0,9, яс~„(0,8-4- 0,4) : як. Таблица 1.1 Конструктивные коэффициенты для ферромагнитных устройств (рис. 1.1)
Нередко в последующих разделах будут встречаться величины- jVc и Nk [см. выражения (1.28), (1.29)]. Они представляют собой относительные периметры сечений поверхностей охлаждения сердечников и катушек соответственно. В заключение отметим, что величины Ус, VK, Пс, Пк, 1с, 1К, Nc и Мк,- характеризующие показатели геометрии ФМУ, имеют в основном смысловую нагрузку и используются для получения конечных выражений оптимизации, содержащих показатели относительных линейных размеров х, у, z и Ks. Конечная цель геометрической оптимизации ФМУ заключается в том, чтобы найти значения х, у, z, Ks и Sc, обеспечивающие наименьший объем, вес или стоимость устройства на единицу мощности. 1.4. Плотность тока и влияющие на нее параметры Чем больше плотность тока в обмотках ФМУ, тем большую мощность будут иметь эти устройства на единицу объема. К сожалению, для плотности тока существуют реальные ограничения, определяемые допустимыми активными потерями мощности ДРК. Потери активной мощности в обмотках ограничиваются в основном тремя факторами: допустимым перегревом катушек тк, потерями напряжения в активном сопротивлении обмоток и оптимальным коэффициентом полезного действия. Каждому из перечисленных факторов будут соответствовать критерии: а)для допустимого перегрева обмоток — см. (1.18а) тк = ДР«/оПкБ„;(1.36) б)для допустимого падения напряжения в активном сопротивлении обмоток~ АиаАРк/Р;(1.37) в)для обеспечения заданного КПД aLz.(138) 7)Pxcoscp Решая (1.36) — (1.38) относительно / с учетом (1.13), (1.23) и (1.25), получим V 1 kss°c \MJx = у»Бк/ркуок Р0-40) h<V пгтг-(М) h<V Pcos<?.(1.42) Г (1 + *)?кк0кКЛ% Поскольку сечение основного магнитопровода ФМУ однозначно определяется выражением (1.11), выражения (1.39), (1.41), (1.42) преобразуются к следующим конечным формам: 4 - У ЮР (1.43) -/«< \/{jJ ЛМАУР/К,,(1.44) где Mju = &uJpKK0Ki(1.45) 4 /„< ]/ \iyMpB,fuYPIKs,(1-46) где AfjT, = Ачхсо5ф(1 + v)p„/c0„.(1-47) В выражениях (1.43), (1.44), (1.46) все значения величин в правой части могут быть предварительно установлены (о значениях #*см. в 1.5). При оптимизации этих величин, например геометрических, приведенные выражения для плотности тока включаются в систему уравнений минимизации заданного удельно-экономического показателя (см. разд. 2.3). Отметим, что приведенные три выражения для допустимых значений плотности тока несовместимы и удовлетворяют - совершенно разным и противоречивым друг другу критериям. Выбирать из них для исследований и расчетов следует то выражение, которое соответствует главному критерию проектирования ФМУ. Два других тогда могут служить как контрольные. Противоречивость формул (1.43), (1.44) и (1.46) очевидна из их структуры. Даже в похожих по форме выражениях (1.44) и (1.46) всегда /,,»/«, так как Л4Л~ (4-~\0)MjU. В обоих из этих выражений по отношению к (1.43) наблюдается обратное влияние мощности и значительно усиленное влияние индукции и частоты. Для СВЧ ФМУ главным ограничением оптимального проектирования является допустимый перегрев. По- 0 1 2 3 4 5 ... 27 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||












