Раздел: Документация
0 1 2 3 4 5 6 7 ... 27 причинам. Во-первых, по требованиям производства, технологии и применения ФМУ их относительные и абсолютные размеры нужно стандартизовать. Во-вторых, два геометрических тела, сочлененных между собой, имеют суммарный минимальный объем только при вполне определенных значениях своих линейных размеров. Второе обстоятельство с дополнением ряда электротехнических и конструктивно-технологических ограничений является основой для стандартизации геометрии ФМУ. Проиллюстрируем влияние геометрии ФМУ на его объем простейшими примерами (более строгие выкладки будут сделаны ниже). На рис. 2.1, а, б, в представлены ФМУ броневого типа, имеющие одинаковые сечения магнитопроводов Sc — ab и одинаковые сечения катушек с обмотками SK=cJhK, что обеспечивает им согласно (2.1) близкую габаритную мощность. Геометрия этих трех ФМУ за счет разных значений /гк и ск при /гкск=const имеет разные формы. Относительно варианта исполнения на рис. 2.1, б геометрия ФМУ на рис. 2.1, а изменена увеличением высоты катушки вдвое при таком же уменьшении ее толщины. Для ФМУ на рис. 2.1, в, наоборот, hK уменьшена-и ск увеличена в 2 раза. Во всех, трех случаях значения сие оставлены без изменений. Объем катушек VK, магнитопровода Ус-и суммарное значение V трех сравниваемых ФМУ оценим по числу элементарных кубических объемов У0, выделенных на рисунках. Получим
Как видно, одно и то же типоисполнение ФМУ при одних и тех же значениях сечения магнитопроводов Sc, сечения катушек 5К и их произведения имеет для разной геометрии неодинаковые значения Ук, Ve и V. В нашем случае ФМУ на рис. 2.1, б обеспечивает меньший суммарный объем активных материалов, чем его варианты 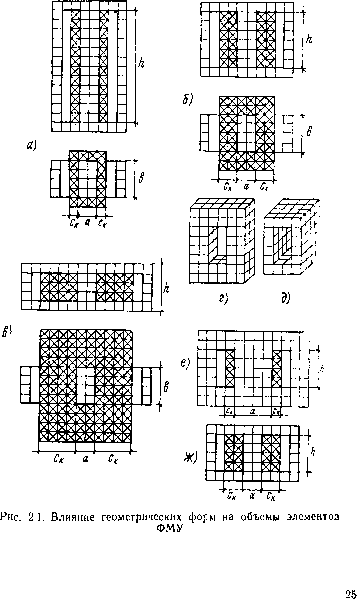 На рис. 2.1, а, в. Просматривается возможность отыскания минимума V, так как Va>V6<.Ve. Отметим, что пока не были использованы все варианты изменения размеров, поскольку сие оставались неизменными. Наличие минимума суммарного объема ФМУ объясняется тем, что изменение линейных размеров этих устройств противоречиво влияет на затр-аты активных материалов для сердечников и катушек. При неизменной мощности уменьшение объема магнитопровода всегда приведет к увеличению объема катушек. На рис. 2.1, г, д показано изменение объема фигуры (она может представлять собой как магнитопроводы, так и катушки) за счет уменьшения длины средней линии при постоянном поперечном сечении. Здесь фигура г имеет 80 элементарных объемов, д — 64 (на 30% мень-•ше), при этом в 2 раза уменьшена ее толщина и увеличена во столько же ширина. Если рассматривать магни-топровод или катушку ФМУ в отдельности, то для уменьшения своего объема они будут стремиться при неизменных SK и 5С вытянуться в тонкостенные фигуры круглой или квадратной формы. Но катушки-находятся внутри магнитопроводов (или наоборот), и-это мешает тем и другим достичь форм минимального объема, указанных выше. Покажем это иа примере. Для ФМУ на рис. 2Л, а, б, в имеем VK = S«LK, LK = 2 (с+Ь+2ск), Vc = ScU, Lc = 4 (a+c+ft).(2.2) В простейшем случае, когда «SK=const и Sc —const, уменьшение VK и Vc возможно лишь за счет уменьшения /-к и Lc. Минимальной LK будет при а—в и с1{->0, но при этом /z-э-оо, так как ск/гк= const, что увеличивает Lc и Ус до со. Наоборот, минимуму Lc соответствует /гк=ск и а->0, что приведет к 6->-оо, так как ab = const, а это даст VK—>-оо. Характер кривых изменения объемов ФМУ при переменных соотношениях b/а и h/c показан на рис. 2.2, а, б. Эти кривые строятся по (2.2) и наглядно демонстрируют наличие минимума общего объема активных материалов ФМУ, достигаемого при определенных значениях L„, Lc и тем самым — при определенных значениях h, с, а, Ь. Нахождение области значений a, b, h, с, соответствующей наилучшим удельно-экономическим показателям ФМУ, является задачей их геометрической оптимизаций. Задача эта сложная и не ограничивается упомянутым выше случаем оптимизации LK и Lc, поскольку на удельно-экономические показатели ФМУ существенно влияют соотношения сечений SK/SC = Ks, поверхности охлаждения катушек и сердечников П0к, П0с, а также другие факторы. v 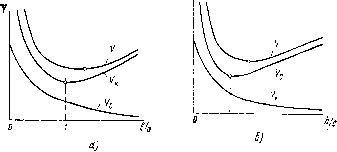 Рис, 2.2. Влияние соотношений размеров ФМУ иа объемы его элементов Например, если у ФМУ на рис. 2.1, е, где 5ке:5Се= = 0,25, уменьшить сечение магнитопровода в 2 раза и во столько же увеличить сечение катушки, что даст исполнение ФМУ на рис. 2.1, ж при 5кж; 5Сж=1, то при неизменных произведениях 5Ке • 5С е=5кж • Sc ж получим У„е=80 V0, Усе=320 V0, Уе=400, Унж=160, VQ, Vcm=l44 V0, 1/ж=304. Таким образом, Уе:Уж>1,3. При дальнейшем увеличении соотношения Sk/Sc объем будет увеличиваться. Здесь тоже при Р= const уменьшение 5К всегда приводит к увеличению 5С и Ус, а уменьшение 5С —к увеличению 5К и. VK. Определенные соотношения 5К и 5С обеспечивают минимальное значение суммарного объема активных материалов ФМУ. Далее будет показано, что величина 7(3=5К/5С является исходной при оптимизации ФМУ. Немаловажную роль в геометрической оптимизации ФМУ имеют поверхности охлаждения сердечников и катушек. Чем больше эти поверхности при том же объеме, тем лучше охлаждение, что позволяет увеличивать плотность тока для катушек, индукцию для сердечников и частоту для питающего напряжения. Все это повышает мощность ФМУ, п если ее увеличение достигнуто в большей мере, чем увеличены VK и Vc, то УЭП устройства улучшаются. Например, ФМУ на рис. 2.1, а имеет больший объем, чем ФМУ н-a рис. 2.1, б, но за счет большей поверхности охлаждения здесь могут быть обеспечены лучшие удельно-экономические показатели, если решающим является ограничение по перегреву. Увеличение поверхностей охлаждения также имеет свои пределы, за которыми УЭП ферромагнитных устройств опять ухудшаются. Так, ФМУ на рис. .2.1, в имеет значительно большую поверхность охлаждения, чем ФМУ на рис. 2.1, а, но геометрия его приводит к увеличениям объемов Ук и Ус, дающих УЭП значительно хуже, чем у ФМУ на рис. 2.1, а, б. В целом для определения параметров оптимальной геометрии ФМУ, обеспечивающей наивыгоднейшие значения удельно-экономических показателей, приходится иметь дело с шестью геометрическими величинами: а, Ь, с, h ~, SK, Sc, что требует или перебора огромного числа вариантов с помощью ЭВМ, или поиска аналитических приемов. В любом случае геометрическая оптимизация ФМУ должна проводиться на серьезной математической- основе. 2.2. Определение геометрии ФМУ методом независимой оптимизации Удельно-экономический показатель по выражению (1.64) включает два функциональных сомножителя э=Мэ ■ v,(2.3} один из которых Мэ зависит от физических величии и геометрических параметров (через / и В*) МКкР-ПМрпВ.и.)**(2.4) другой v — от соотношений геометрических размеров + - + дКс+рКн].(2.5) Сомножитель v можно минимизировать независимо от М3 и установить при этом обобщенно оптимизированные для всех возможных ограничений показатели геометрии Кь, Кс, Kh и Ks. Определяемую ими геометрию назовем независимой. Поскольку физические величины показателя М3 не связаны с геометрией, а входящие в него значения величин / и В* найдутся по соответствующим выражениям, например, по (1.58) и (1.59), (2.23) и (2.24) и другим, учитывающим после оптимизации Кь, Кс, Kh как геометрию, так и установленные для проектирования ограничения, то задача оптимального расчета ФМУ в целом будет решена. Прием определения значения параметров геометрии через минимизацию v по выражению (2.5) нами назван методом независимой оптимизации ФМУ. Он дает усредненные показатели оптимальной геометрии ФМУ для всех возможных ограничений. Имеются частные случаи метода с оптимизацией геометрии для конкретных ограничений. При этом возможно некоторое улучшение УЭП против их значении для ФМУ с независимой геометрией. О таких вариантах будет сказано в разд. 2.3 и 2.4. Величина v является безразмерной и может быть названа показателем геометрии.. Если учесть, что откул л Ks~ch/Sc~Kh- ■ Кс Кс — КМн, или Kh = Ks/Kc, (2.7) (2.8) то даже по внешнему виду выражения (2.5) очевидно наличие минимумов для v по каждой из переменных Кг, Kh, Кь и К,. Это позволяет иметь систему уравнений: dv;dKb = r0Ksn - (r0Ksm + т) К;2 = О dvidKc = r0Ksq + q-pKsKc = 0; dv/дКп =--P-Ks (r0Ksq + q) Kl = 0, откуда получим (2.9) 1 т т п rQKsn Kco = VpKsl(r0Ksq + qh (2.10) (2.11) 29 0 1 2 3 4 5 6 7 ... 27 |












