Раздел: Документация

0 ... 2 3 4 5 6 7 8 ... 27

(2.12)

где Кьо, Ксо, Kho — оптимальные значения относительных размеров ФМУ, обеспечивающих минимальный коэффициент геометрии v.

Подставляя Къ = Кьо, Кс—Каа, Kh—Kho по (2.10) — (2.12) в выражение (2.5), получим уравнение кривой v=f (Ks), определяющей влияние на УЭП одного из важнейших для оптимального проектирования ФМУ показателя Ks=SQK/Sc,

v = 2rK7]li[]/ nmr0[r0Ks-\- +

+ ]/pq{r0K, + q-~j .(2.13)

Кривые по выражению (2.13) являются непрерывными, имеют область минимальных значений: в обширной зоне для Ks и строятся в виде семейств для параметра г0, который меняется в значительных пределах от 5 до 0,1 (см. данные табл. 2.1 и кривые на рис. 2.3) для броневых ФМУ.

Таблица 2.1 Кривые v=f(Ks) для броневого ФМУ (рис. 1.1, в)

	Значения Ks
Го	0,1	0,2	0,3	0,4	0,6	0,8	1	1,4	1,8	2,4
0,5 1 2	12,1 16,4 18,3	10,4 14,5 16,8	9,7 9,4 8,9 8,7 13,8 12,0 11,7 11,7 16,5 16,5 16,8 17,2				8,6 11,8 17,6	8,5 12,0 18,4	8,6 12,2 19,0	8,7 12,7 20

Выражение (2.13) достаточно точно аппроксимируется более простой формулой

(2.14)

где

v = А.У(г0К, + *)2, А = 2r (V~mnr+ Vfq).

(2.15) (2.16)

На рис. 2.3 пунктиром показаны кривые, построенные по (2.14), и сплошными линиями — по (2.13). Нулевая частная производная для (2.14) дает

r0Ks=a,

откуда

Kso = a/r0.(2.17)

Имея оптимальные значения Kso по (2.17), нетрудно найти соответствующие ему Кьо, Ксо и Kho по (2.10) — (2.12). Оптимальные соотношения размеров для незави-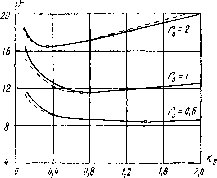

Рис. 2.3. Кривые зависимости г.еомет, рического показателя v от соотношения сечений /Cs=jS0k/Sc при независимой геометрий ФМУ

снмой геометрии типовых ФМУ на рис. 1.1 с конструктивными коэффициентами по табл. 1.1 приведены в табл. 2.2. Перейти от Кь, Кс и Кь. к показателям относительной геометрии, принятым в технической литературе (х, у, z), несложно, поскольку после соответствующих преобразований в (1.21) с учетом (1.19) будем иметь:

у = К1, х = КсКь; г = КАКЬ,

или Kb = Vy, Кс = х/Уу, Kh=z\\fy, Ks= -

У

Не останавливаясь на их анализе, поскольку он будет сделан в последующих разделах, отметим следую-

(2.18)

---

щие особенности независимой геометрии ФМУ, присущие практически всем ограничениям.

Таблица 2.2

Оптимальные показатели независимой геометрии конструкций ФМУ на рис. 1.1 при Гц—\

Позиции на рнс. 1.1	в	д	е	ж	3	а	б	г
Kho	1,4	1,1	1,1	2,1	1,3	1,7	1,7	—
Ксо	0,5	0,5о	0,55	0,8	0,8	0,65	0,8	1,2
Kso	0,7	0,6	0,6	1,7	1	1,1	1,4	1
а	0,7	0,6	0,6	1,7	1	1,1	1,4	1
Уо	2,1	2,4	2,4	2	1,8	2,4	2,1	2
Хо	0,72	0,85	0,85	1,1	1,1	1	1,2	1,7
2о	2	1,7	1,7	3	1,7	2,5	2,5	—

1.Параметр Кьо остается неизменным для всех значений г0

Кьо = Ут\п + т/ап.

2.С увеличением г0 значения Км и Ксо в одинаковой мере уменьшаются и, поскольку

Кю = V*}pr0(a9-\-q), Кс(1 = Vp«lrQ{°-q + q)-

3.Если As0=const, то с изменением Kho обратно пропорционально этому параметру изменяется величина КсО

Kso = КсО Kho-

4.Поскольку области минимальных значений кривых v=f(Ks, г0) не являются узкими, то значение Kso необязательно однозначно подсчитывать по (2.17). Можно выбирать Kso в пределах /С8омин</(во<Квомак, соответствующих двум значениям у~1,05 умин по кривой (см. рис. 2.3).-Это расширяет возможности решения конструкторских, технологических и стандартизационных вопросов.

2.3. Влияние на геометрию плотности тока и индукции

Выражение для удельно-экономических показателей ФМУ (1.64) с учетом (1.10), (1.40), (1.43)— (1.57) по-35

казывает, что из физических величин с геометрией связаны лишь плотность тока и индукция. При этом на геометрию эти величины влияют неоднозначно. При заданных потерях в стали или токе намагничивания максимальное значение индукции достигается при наименьшей средней линии магнитопровода. Увеличение плотности тока с ограничением потерь мощности или напряжения в катушках достигается минимизацией объема обмоточного материала, то есть путем уменьшения сечения и средней длины катушек. Совершенно противоположно влияет геометрия на увеличение индукции и плотности тока при ограничениях по нагреву ФМУ. Здесь должны быть развитыми поверхности охлаждения, что потребует вариации всех трех относительных размеров — х, у, z. В свою очередь, как отмечалось в 2.1, минимумудельно-экономического показателя достигается только при вполне определенных значениях 1К, 1С и К,.

В связи с изложенным показатели независимой геометрии ФМУ корректируются в зависимости от того, каким главным критериям должно удовлетворять проектируемое устройство. Взаимосвязь индукции, и плотности тока с параметрами геометрии и их влияние на удельно-экономический показатель в соответствии с (2.4) следует оценивать сомножителем

У= (/Б*)-за.(2.19)

Выражение для этого сомножителя не может быть однозначным, поскольку не существует однозначных выражений для плотности тока и индукции. Одна пара формул для / и В*, удовлетворяющих требованию обеспечения допустимого перегрева ФМУ, приведена в разд. 1.5 [см. (1.58) и (1.59)]. Решая совместно (1.50), (1.54), (1.56) и (1.43),. (1.44), (1.46) в различных сочетаниях в зависимости от намечаемых ограничений для проектируемых ФМУ, можно получить другие пары выражений для / и В*. Приведем некоторые из них с соответствующими показателями У.

Если расчетные значения плотности тока и индукции должны обеспечивать заданный КПД, то решаются совместно (1.46) и (1.56) t что дает

У, = V [(-К~;(2.20)

---

5/?Г

(2.21)

где Y, = {lAYWf•(2-22)

При расчете индукции по заданному перегреву сердечников и плотности тока по заданным потерям напряжения будем иметь

£*тси —

(2.23) (2.24)

Yiji = (Bzcuj*cu)-

-3/4 ;

4

(2.25)

3/4, ,,3/4

где YXc„ = lTlN

При расчете индукции в сердечнике с зазором б по заданному току намагничивания го% и плотности тока по заданному перегреву катушек %к

(2.26) (2.27)

(2.28)

V, = VVoVo/S)7 {K,Mf<NK)> (P!Mpfvf;

ю.-

•Лк1м = 7hK0KnJi*Mp {MjzNKflbPKU

где 4TVo» = Л°/5Л/70,68°6.

Для обеспечения заданного перегрева катушек и сердечников имеем (1.58), (1.59) и соответственно

к с / л* л,г лг Л/ \2 Л/f

где WKKNJV.

34

(2.29) (2.29а)

Не останавливаясь на выражениях / и В* для других, мало распространенных случаев их расчета, сделаем некоторые выводы о влиянии этих величин на УЭП через геометрические параметры, составляющие показатель гр по (2.22), (2.25), (2.28), (2.29).

Предварительно отметим, что при изменении значений Кс, Kh, Кь в пределах 0,5-4-2 раза от их оптимальных величин для независимой геометрии, определяемых по выражениям (2.1.0) — (2.12), имеем К„ » Кс, /к const, Nc ~ const, /с = Kh, NK = Kh. (2.30)

С учетом (2.30) получаем Wv = const, Wn = KJ*• Kh, *?Vo8 = Ku/5IKl6,(2.31)

wVc=\iK°n25.

Согласно (2.31) оптимальная геометрия повторяет независимую лишь в случае проектирования ФМУ по заданному перегреву сердечников и заданным потерям напряжения, поскольку \ptc„ ~const. При обеспечении заданного КПД, параметры независимой геометрии следует корректировать, уменьшая Кно с небольшим" изменением соотношения сечений Kso, так как грвз = ft/Cs0,25. В случаях, когда при проектировании ФМУ приходится учитывать перегрев катушек тк, показатели независимой геометрии меняются, в основном, путем увеличения Км-

В целом определение координат минимума геометрического показателя v с учетом составляющей гр осложняется, и не во всех случаях прием частных производных решает эту задачу. Тогда приходится вводить ограничения или пользоваться графоаналитическими приемами. Авторами разработана для таких случаев методика, базирующаяся на корректировке предварительно найденных оптимальных параметров независимой геометрии ФМУ. Основные положения этой методики следующие.

1.* Выражение показателя геометрии для заданных ограничений проектируемого ФМУ

= Ф,(*А + /с)*Г3/4(2.32)

записывается с учетом коэффициентов корректировки Kl, Кдс, Kt, Kt:

0 ... 2 3 4 5 6 7 8 ... 27