Раздел: Документация
0 ... 4 5 6 7 8 9 10 ... 17 Исследования показывают, что вес и размеры дросселя почти обратно пропорциональны магнитной индукции насыщения выбранного ферромагнетика и обратно пропорциональны величине удельных потерь. Требование стабильности характеристик вызвано условиями эксплуатации дросселей и, в частности, например, тем, что сети повышенной частоты дают обычно энергию плохого качества — частота колеблется в широких пределах. Требования в отношении малой стоимости и технологичности часто являются определяющими при выборе ферромагнетика для сердечников дросселей массовой аппаратуры. Лучшими современными отечественными материалами для сердечников низкочастотных дросселей (с частотой до 1 ООО гц) следует признать холоднокатаные стали марок Э310—Э380. Перспективным является и новый материал — супермендюр 49КФ-ВИ (ЭП-581). Для высокочастотных дросселей в ряде случаев можно рекомендовать ферриты. Для сердечников дросселей с частотой 50 гц целесообразно применять сталь Э380 с толщиной листа 0,2— 0,35 мм. При этой стали габариты сердечников на 20— 25% меньше, чем сердечников, сделанных из стали Э310, а их вес меньше на 15—20%. Для сердечников дросселей с частотой 400 гц следует применять сталь с толщиной листа в 0,15—0,2 мм. Для сердечников высокочастотных дросселей с частотой, превышающей 1 000 гц, можно рекомендовать марганец-цинковые и никель-цинковые ферриты, например феррит 4000 ИМ и 2000 ИМ. Достоинством их является высокое удельное электрическое сопротивление и, следовательно, малые потери на вихревые токи. ТЕОРИЯ РАБОТЫ ДРОССЕЛЯ ПЕРЕМЕННОГО ТОКА С НЕЛИНЕЙНЫМ ФЕРРОМАГНИТНЫМ СЕРДЕЧНИКОМ 3.1. Общие замечания В этой главе излагаются основы теории дросселя и, в частности, рассматриваются процессы в нем при установившемся и переходном режимах. При этом описываются как аналитические методы исследования, так и численные, основанные на широком использовании ЭЦВМ. В результате предлагается уточненный метод расчета электромагнитного режима дросселя с учетом качественного характера нелинейности его ферромагнитного сердечника, потерь в стали и особенностей работы в той или иной конкретной электрической цепи. Все расчеты базируются на нелинейных магнитных характеристиках сердечника. При этом в качестве исходных данных достаточно иметь зависимости Вт(Н) и РСу(Вт), снятые на опытном образце дросселя без зазора в маг-нитопроводе, в режиме синусоидальной магнитной индукции. При рассмотрении отдельных вопросов будем пренебрегать неравномерностью распределения магнитного потока по площади поперечного сечения сердечника, зависимостью магнитных свойств сердечника от его конфигурации, формой кривой тока, температурой и емкостью между витками обмотки дросселя. Приведенные теоретические сведения позволят читателю лучше уяснить ряд явлений и зависимостей, знание которых необходимо для правильного определения электромагнитного режима и параметров дросселя и обоснования более строгой методики его расчета. Отдельные параграфы главы рассчитаны лишь на специалистов и могут быть опущены теми читателями, для которых представляет интерес только метод проектирования дросселей, приведенный в пятой главе книги. 3.2. Связи между электрическими и магнитными величинами в дросселе с нелинейным ферромагнитным сердечником. Эквивалентный дроссель При расчете дросселя и исследовании процессов в нем важно знать метод определения электромагнитных параметров. В частности, нужно находить ток дросселя по известному напряжению (прямая задача) или напряжение по известному току (обратная задача) и затем по этим данным определять нужные электромагнитные параметры дросселя. Эта задача для простого линейного индуктивного элемента решается сравнительно просто— необходимо воспользоваться понятием индуктивности. Для дросселя же с ферромагнитным сердечником из-за нелинейных свойств последнего связь между напряжением и током устанавливается через магнитные характеристики сердечника. Установлению некоторых связей посвящен данный параграф. Связи между электрическими и магнитными величинами для дросселя с ферромагнитным сердечником можно получить на основе рассмотрения нелинейного дифференциального уравнения +(3.1) где т1 = /(0-(3-1) Здесь и, i — мгновенные значения напряжения и тока; г, Ls — активное сопротивление обмотки и индуктивность рассеяния; ilp — мгновенное значение потокосцепления. Как видим, в дросселе с ферромагнитным сердечником связь между напряжением на его зажимах и током в обмотке обусловливается магнитной характеристикой сердечника, что значительно усложняет математический анализ дросселя и его расчет. 44 Для установления принципиальных зависимостей рассмотрим простейший дроссель, в котором активное сопротивление обмотки и индуктивность рассеяния невелики и, следовательно, ими можно пренебречь. Установим связь между электрическими и магнитными величинами для идеального и идеализированного дросселей. Под идеальным дросселем будем понимать дроссель без активного сопротивления обмотки, без индуктивности 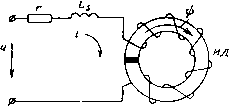 Рис. 3.1. Схема электрической цепи дросселя. т — сопротивление обмотки дросселя; Ls — индуктивность рассеяния; ИД — идеальный или идеализированный дроссель. рассеяния и без потерь в сердечнике, под идеализированным— тот же дроссель, но с потерями в сердечнике. Идеальный и идеализированный дроссели физически не осуществимы, но их введение в анализ существенным образом упрощает некоторые взаимосвязи и вместе с тем позволяет более углубленно проанализировать свойства дросселя с учетом данных его обмотки или параметров электрической цепи, в которую он включен. Электрическую цепь дросселя будем изображать как бы состоящей из последовательного соединения линейного активного сопротивления, линейной индуктивности и идеального или идеализированного нелинейного дросселя. Такая схема дана на рис. 3.1 и соответствует приведенному выше дифференциальному уравнению дросселя. Схема позволяет порознь рассмотреть идеальный, идеализированный и реальный дроссели. Для придания общности анализу будем широко пользоваться понятием об эквивалентном дросселе. Под эквивалентным дросселем подразумевается дроссель, имеющий одну обмотку и один сердечник. Витки обмотки эквивалентного дросселя соединены друг с другом последовательно. Получаемые результаты при этом мо- гут быть распространены и на случай, когда обмотка имеет параллельные ветви. Так, обмотка с двумя параллельными цепями может быть заменена одной с числом витков, в два раза меньшим общего числа витков двух цепей, и с током, большим в два раза. Ниже определяются соотношения величин для идеального и идеализированного дросселей с зазором и без него и для дросселя, включенного в электрическую цепь. 1. Идеальный и идеализированный дроссели без зазора Математическое описание процессов в ферромагнитном сердечнике и обмотке таких дросселей, как следует из (3.1) и (3.1), в сущности, может быть проведено с помощью трех основных уравнений: u = ws -jj,(3.2) h = f(b),(3.3) §hdlc=Xiw,(3.4) где h и b — мгновенные значения напряженности поля и магнитной индукции в сердечнике; /с s — длина средней магнитной линии и активное поперечное сечение сердечника; w — число витков дросселя. Первое из этих уравнений отражает закон электромагнитной индукции, второе — взаимосвязь магнитных величин или, иначе, свойства ферромагнитного сердечника и третье — закон полного тока. Последовательность решения уравнений (3.2), (3.3) и (3.4) можно отразить следующей схемой: Стрелками слева направо показан порядок решения прямой задачи, а справа налево — обратной. Из схемы видно, что в отличие от простого линейного индуктивного элемента [44] исследование в дросселе с ферромагнитным сердечником основано на включе-46 нии в число математических связей уравнений, отражающих взаимосвязь магнитных величин, т. е., в конечном счете, свойств ферромагнитного сердечника. Рассмотрение уравнений (3.2), (3.3) и (3.4) и схемы, определяющей порядок их решения, дает возможность представить физический процесс в обмотке и сердечнике идеального и идеализированного дросселей. Он сводится к следующему. Под действием напряжения, приложенного к дросселю от какого-либо источника переменного тока, по обмотке проходит ток, который создает в сердечнике переменное магнитное поле. В свою очередь, это поле в соответствии с законом электромагнитной индукции создает в обмотке дросселя э. д. с. самоиндукции, направленную встречно току и уравновешивающую приложенное напряжение. Ток при этом устанавливается такой величины и имеет такой характер изменения во времени, что образуемое им магнитное поле индуктирует э. д. с. в обмотке в строгом соответствии с величиной и характером приложенного напряжения. Другими словами, каждому мгновенному значению напряжения, приложенного к зажимам дросселя, соответствуют строго определенные мгновенные значения магнитной индукции и, следовательно, напряженности поля и тока. Основной трудностью при исследовании процессов в дросселе является изучение взаимосвязей между различными магнитными величинами, обусловленных уравнением (3.3). Эта задача, обычно нелинейная, представляет собой самую важную и вместе с тем самую трудоемкую часть общей задачи по изучению дросселя. Этому вопросу уделено особое внимание в § 3.4—3.8. Здесь лишь отметим, что в идеальном дросселе каждому мгновенному значению магнитной индукции соответствует вполне определенное мгновенное значение напряженности поля и, наоборот, каждому мгновенному значению напряженности поля — вполне определенное мгновенное значение магнитной индукции, и поэтому при известной форме кривой магнитной индукции можно определить кривую напряженности поля, а по известной форме кривой тока — форму кривой магнитной индукции. Для каждой из этих конкретных форм можно установить нужные для расчетов взаимосвязи между их интегральными характеристиками. Для идеализирован- 0 ... 4 5 6 7 8 9 10 ... 17 |












