Раздел: Документация
0 ... 7 8 9 10 11 12 13 ... 17 Удельные потери в сердечникедросселя за один период изменения напряжения равны тт Рсу = ф Kdb = J h&dt = j KVdt, (3.23) и0 где /га — мгновенное значениеактивной слагающей напряженности поля. 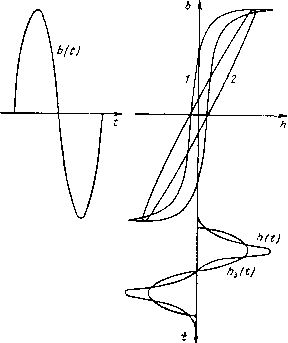 Рис. 3.6. Замена действительной петли расчетной эллиптической: 1 — действительная петля; 2 — эллиптическая. Как следует из этого выражения, удельные потери в сердечнике определяются произведением э. д. с, наводимой основным магнитным потоком, на напряженность магнитного поля. Из выражения (3.23) вытекают следующие соотношения для удельных мощностей различных гармоник: -sr= —2—sin №1 — ?0 + n + s k В*т"ьт sin-y,).(3.24) A=3, 5. Первый член в формуле (3.24) представляет собой удельную мощность первой гармоники, второй — сумму удельных мощностей высших гармоник. Из формулы (3.24) следует, в частности, что при питании реального дросселя синусоидальным напряжением активная составляющая основной гармоники тока обусловлена не только потерями в ферромагнетике сердечника и в проводе обмотки от основной гармоники магнитного потока и тока, но также и преобразованием части энергии колебаний основной частоты в энергию колебаний более высоких частот. Энергия высших гармоник рассеивается в виде потерь в обмотке. 3.3. Схемы замещения и векторные диаграммы идеализированного дросселя Рассмотрение схем замещения и векторных диаграмм всегда позволяет глубже понять физические процессы, описываемые математически, что особенно важно при нелинейном дросселе, напряжение и ток которого, оба или в отдельности, могут быть несинусоидальными. Особый интерес для уяснения всего последующего материала представляют схемы замещения и соответствующие им векторные диаграммы нелинейного звена, изображенного на рис. 3.1. Рассмотрение внутренней структуры этого звена позволяет глубже понять процессы, протекающие в реальном дросселе, и обосновать метод его электрического расчета. Сделаем это для идеализированного дросселя, который в частном случае может отображать и идеальный дроссель. Рассмотрение идеализированного дросселя особенно интересно, так как в реальных дросселях омическое сопротивление обмотки и индуктивность рассеяния малы и ими можно часто вовсе пренебречь. Если же этого сделать нельзя, то параметры г и Ls всегда можно отнести к цепи нагрузки и учесть их влияние при расчете устройства в целом. Правомерность и возможность применения схем замещения и векторных диаграмм для нелинейных элементов обосновывается, в сущности, методом двухполюсника и теоремой о компенсации [64]. Согласно им анализ процессов, протекающих в обмотке дросселя и в его магни-топроводе, можно в значительной мере упростить, если рассматривать процессы относительно входных величин напряжения и тока. Нелинейный дроссель следует представить в виде нелинейного пассивного двухполюсника. После этого для каждой гармоники входного тока или напряжения можно построить схему замещения и соответствующую ей векторную диаграмму. Подчеркнем, что как схемы замещения, так и векторные диаграммы для нелинейных величин можно строить только отдельно для каждой из составляющих гармоник. Нанесение на одну плоскость векторов всех гармоник не дает возможности производить операции с векторами, поэтому будем пользоваться и так называемыми ориентационными диаграммами [10]. Совокупность схем замещения для каждой из гармоник векторных и ориен-тационных диаграмм весьма полезна при расчетах нелинейных дросселей. 1, Схемы замещения и векторные диаграммы электрической цепи идеализированного дросселя Напряжение и ток по каждой из гармоник на входе дросселя, как было установлено в (3.2), связаны законом Ома: Uk=Zh!k, ik--=YkUk,(3.25) где Z& и Yh — комплексные значения входного сопротивления и проводимости обмотки дросселя по k-й гармонике. Для идеализированного дросселя и Yh обусловлены лишь электромагнитными процессами в сердечнике (r=0, Ls — 0), т. е. той э. д. с, которая наводится в ре-62 зультате ответной реакции потока при прохождении тока по обмотке, и поэтому для него имеем zfc = yJ-=/w;.(3.26) Поскольку Lh в выражении (3.26) — величина комплексная, то Yh и Zft — также комплексные величины. Другими словами, идеализированный дроссель является не чи-  Рис. 3.7. Схемы замещения электрической и магнитной цепей идеализированного дросселя без зазора в магнитопроводе: а — последовательная схема электрической цепи; б — параллельная схема; в — параллельная схема магнитной цепи; г — последовательная схема. сто индуктивным элементом, а элементом, в котором имеют место и потери энергии. Поэтому для исследования такого дросселя удобно применить схемы замещения, которые характеризовали бы не только его индуктивные свойства, но и процессы, обусловливающие нагрев сердечника. Разумеется, схемы замещения должны соответствовать уравнениям (3.25). Первое уравнение удобно отображать последовательной схемой замещения, второе—параллельной. Такие схемы приведены на рис. 3.7,а и б. А. Последовательная схема замещения электрической цепи идеализированного дросселя. Эквивалентное сопротивление обмотки идеализированного дросселя при переменном токе произвольной формы можно представить по каждой из гармоник в следующем виде (индекс «k» для сокращения записи будем опускать): Z = — = z cos f-j-jzsitif—r-j-jx, где г=гй и х=хс— эквивалентное активное и соответственно реактивное сопротивления идеализированного дросселя, обусловленные процессами в стали. В свою очередь, комплексы напряжения и тока по каждой из гармоник для этой схемы можно представить в виде / = /, L/ = L/ey<p = L/cos? + yL/sm?=L/a + yL/p. Соответствующие для этих уравнений схема замещения и векторная диаграмма представлены на рис. 3.7,с и 3.8,а. Как видим, при последовательной схеме замещения ток принят за основной вектор и его направление оовпадает с осью вещественных величин. Напряжение на дросселе при данной схеме по каждой из гармоник представляется состоящим из двух слагающих: активной Ua и реактивной Up. Активную слагающую Ua можно рассматривать как падение напряжения на каком-то эквивалентном активном сопротивлении, характеризующем потери в стали, а реактивную £/р — на каком-то реактивном сопротивлении. Каждая из них обусловлена электромагнитными процессами в сердечнике дросселя. Периодическое изменение магнитного потока в сердечнике создает активное и реактивное падения напряжения в обмотке дросселя. Еще раз подчеркнем, что первое из падений напряжения характеризует потери в стали, второе — индуктивность дросселя. При протекании через обмотку дросселя синусоидального тока схема замещения электрической цепи для основной гармоники и соответствующая ей векторная диаграмма имеют тот же вид, что и на рис. 3.7,а и 3.8,а. Высшие гармоники напряжения при этом могут рассматриваться как результат действия э. д. с, вызванной синусоидальным током. Схема замещения по -м гармони-64  J
Рис. 3.8. Векторные диаграммы идеализированного дросселя без зазора в магнитопроводе: а — для последовательной схемы электрической цепи; б — для параллельной схемы; в — для параллельной схемы магнитной цепи; г — для последовательной схемы.
U 1 dp \u3dp i>7dp Undp oar Bsm Взт \Вцт four °jm D,m 1 *1 a) Ugdp Usdp 6) Рис. 3.9. Диаграммы ориентации гармоники; а — при синусоидальном потоке; б — при синусоидальном» токе. 0 ... 7 8 9 10 11 12 13 ... 17 |
|||||||||||||||||||||||||||||||||||||||












