Раздел: Документация
0 ... 10 11 12 13 14 15 16 17 где h~ b — мгновенные значения напряженности поля и магнитной индукции; h°, Ь° — то же в относительных безразмерных величинах. При второй системе относительных единиц кривая намагничивания приводится к единичному масштабу. При этой системе одна из точек кривой намагничивания принимается за базисную (Вбаз, //баз), а координаты всех других точек выражаются относительно этих базисных параметров. В качестве базисных непременно должны быть выбраны такие значения #баз и баз, которые находятся в конце рабочего участка кривой намагничивания сердечника. Лишь при таком выборе могут быгь найдены оптимальные значения коэффициентов аппроксимаций, соответствующих нужному рабочему участку. Рабочие участки, или рабочие области, для дросселей с сердечниками из электротехнической стали при аппроксимации реактивных кривых намагничивания следующие: от 0 до 1 ООО или до 2 500, 5 000, 10 000, 25 000 а/м. Опишем, как могут быть найдены оптимальные значения коэффициентов аппроксимирующих выражений, наилучшим образом соответствующие рабочему участку какой-либо конкретной кривой намагничивания. Проще всего это сделать, пользуясь полученными нами с помощью ЭЦВМ зависимостями, представленными на рис. 3.15. Зависимости построены по следующим формулам: при аппроксимации кривой намагничивания гиперболическим синусом Sh(&*/3*6a3),оо7Ч при аппроксимации кривой намагничивания круговым синусом I.* sin (£*аВ*баз) Sin В* (3.37) где В*баз—показатель нелинейности кривой намагничивания (рис. 3.15). Способ определения оптимальных коэффициентов аппроксимирующих выражений сводится к следующему. Для базисных значений //баз и #баз кривую намагничивания, подлежащую аппроксимации, следует привести к единичному масштабу и нанести на кальку в том же 78 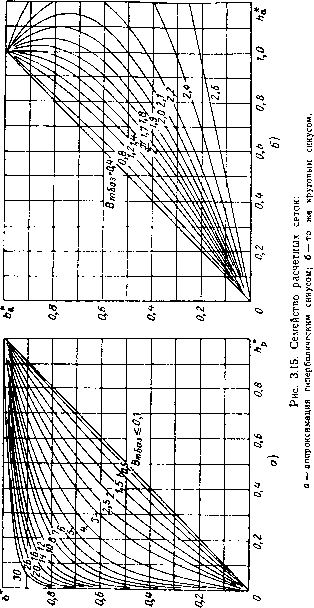 масштабе, что и кривые сеток (рис. 3.15). Путем совмещения кальки с кривыми сеток подбирается наиболее оптимальная величина показателя нелинейности В*баз- Поиск наивыгоднейшего значения В*баз и коэффициентов аир можно произвести и аналитически, например методом наименьших квадратов, минимизацией выражения N A=E№)-ft°№ (3-38) i=i ° где N— число заданных точек на реальной кривой; h0(bi) и h(bi) —заданная и аппроксимирующая функции. Оптимальная величина В*баз находится следующим порядком. Первоначально следует принять В*баз=1Д Из условия необходимости привязки аппроксимирующей зависимости к заданной базисной точке (Ябаз, баз) можно определить величину коэффициента а и затем по выражению (3.38)—величину ошибки. По методу прямого спуска [13] путем изменения величины В*баз можно определить ее оптимальное значение, соответствующее минимуму ошибки. Далее определяются коэффициенты искомой конкретной функции Н баз 01 ~" Sh /3*6а3 (3.39) О Д*баз #баз Нахождение оптимальных значений коэффициентов аппроксимирующего выражения графическим методом лучше всего пояснить на конкретном примере. Пример. Определить коэффициенты аппроксимации кривой намагничивания сердечника нз электротехнической стали Э310 при выражении ее гиперболическим синусом. Данные кривой намагничивания приведены в табл. 3.1. Выберем соответственно данному рабочему участку кривой намагничивания следующую базисную точку: #баэ=5 000 а/м, Вбав= =2,017 тл. В единичном масштабе кривая намагничивания отражается числами, приведенными в табл. 3.2. Нанесем зависимость h*=f(b*) на кальку и совместим кальку с рис. 3.15. Найдем величину В*баз, определяющую степень нелинейности рабочего участка кривой намагничивания: В*вав=13. Отсюда коэффициенты аппроксимации Я баз5000 а= shB*6a3 =1ГГз-=00226 «/*• „ В*«аз 13 Рабочий участок кривой намагничивания оптимальным образом описывается следующим выражением: Л = 0,0226 sh 6.,44 b.(3.40) 3.5. Математическая модель семейства динамических гистерезисных петель. Использование модели для решения задач гармонического анализа Предложенное в предыдущем параграфе уравнение для выражения семейства статических гистерезисных петель позволяет получить ориентировочную структурную математическую модель для описания семейства динамических петель гистерезиса. Для этого нужно лишь учесть составляющие потерь на вихревые токи *. При установившемся режиме периодического намагничивания математическая модель, выражающая семейство динамических гистерезисных петель, в параметрической форме записи может быть представлена в виде 2п+\ Л = ЛС + ЛЙ,(3.41) ftc= ар (Bm) sh pp (Bm) b±ar (Bm) sin pr (Bm) ]/ B*n — b* , Здесь Bhm— амплитудное значение k-й гармоники магнитной индукции; Строго говоря, нужно учитывать и дополнительные составляющие потерь на вязкость, последействие и т. д. Однако для рассматриваемых нами низкочастотных дросселей этими составляющими можно пренебречь. Учет таких потерь подробно изложен, например, в {61]. фй—начальная фаза k-й гармоники; Вт — максимальное значение кривой несинусоидальной магнитной индукции; Лв — составляющая напряженности ноля, обусловленная вихревыми токами; г и — коэффициент, зависящий от свойств материала ферромагнитного сердечника и от размеров сердечника. Величина гв может быть определена по известной формуле где Y — удельныйвес материала; Л» — удельные потери на вихревые токи при заданном режиме намагничивания. При синусоидальном характере изменения Ъ модель может быть несколько упрощена. Действительно, при b=Bmsm at гистерезисная составляющая напряженности поля Лг (3.33) может быть представлена в виде Аг = ar (Вт) sin рг (Вт) -jj- Ь, где Ь — производная от магнитной индукции по времени. Сопоставляя полученное выражение с формулой для hB, можно увидеть, что Лг и Лв обусловливаются производной от магнитной индукции по времени. Отсюда активные процессы ориентировочно можно представить в виде h, = <i,(Bm)sm(Bm)b,(3.33") где аа (Вт), % (Вт) — коэффициенты аппроксимации динамической петли гистерезиса. Уравнения гистерезисной петли от величины Вт при этом имеют вид 6 = Bmsm Ы, h = ар (Вт) sh рр (Вт) Ь 4- аа (Вт) sin ра (Вт) У. (3.42) Рассчитанные по этим уравнениям гистерезисные петли J73] даны на рис. 3.14,6. Как видим, расчетные петли хорошо согласуются с опытными. 6*83 0 ... 10 11 12 13 14 15 16 17 |












