Раздел: Документация
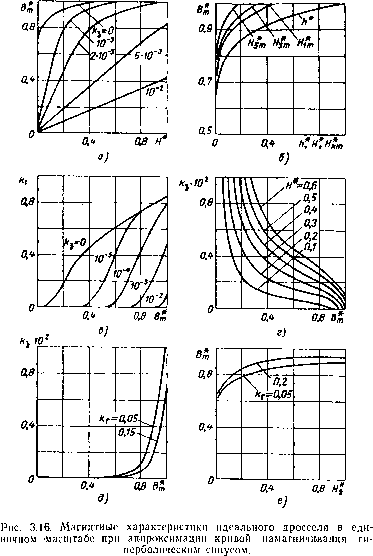
0 ... 11 12 13 14 15 16 17 Модели, предлагаемые для выражения процессов намагничивания ферромагнетика, могут быть положены в основу расчета любых цепей с дросселями и при самых различных установившихся режимах. Для этого нужно определить коэффициенты ар, рр, аг, рг. Л> (или аа, ра) для всех ожидаемых режимов работы ферромагнетика и затем их аппроксимировать. При этом можно получить петли не только в зависимости от магнитной индукции, как это было показано, но и от других факторов (температуры, частоты тока и т. д.). Использование таких моделей, очевидно, приведет к более точным методам расчета дросселей. Модель очень удобна для решения задач гармонического анализа. В частности, с помощью этой модели удается аналитическим путем определить гармонический состав кривой напряженности поля, среднеквадратичное значение кривой h и потери в стали. 1. Определение гармонического состава кривой напряженности поля Гармонический состав кривой h может быть определен следующим образом. Выразим амплитудные значения k-x гармоник напряженности поля формулами Фурье Нктр = -у1 j hp (t) sin Ы dt, о г ftma = -у- J ha (t) COS ktat dt. 0 Заменяя в них hv(t) и /га(г) соответствующими значениями из (3.33) и (3.33")* и учитывая закон изменения для Ь имеем г flftmp = — \ <*psh $рВт sin <ot sin k«>t dt, oJ(3-43) T 2 Г Нцтц = — I <zasin j3afl,„COSai£ COskuttdt. . 0 * Для упрощения формы записи уравнений зависимости ар, рр, аа и ра от величины Вт не указываем. 84 Интегралы такого вида, как известно, подсчитывают через функции Бесселя. Действительно, из [13] известно */2 Лп {х) = — 1 cos (х sin <р) cos 2n<p d<f, П „J(3.43) ■к ft Jzn+1 (х) = — J sin (x sin <p) sin (2n -J- 1) <p d?. 0 Отсюда, сопоставляя (3.43) с (3.43) и учитывая известные соотношения In{x)= jnJn{jx), sh/z=/sinz, можно получить 2л+ 1ft-1 ЛР= 2ap Yi (— 1) 2 h{%Bm)smkot, (3.44) 2л+ 1ft—1 К = 2аа (— 1) 2 Л (hBm) cos Ы, ft=l где /ft — функция Бесселя первого рода от мнимого аргумента с целым вещественным индексом k (k-то порядка); Д — функция Бесселя первого рода от действительного аргумента с целым вещественным индексом k (k-то порядка). Отсюда первая, основная, гармоника равна // imp = 2a.pl! фрВт), //ima = 2aayt ($лВт), третья гармоника fi3mpz= 2<3tp/3 (ppfim), //зта= 2ааУ3 $&Вт), пятая гармоника Н5тр — 2а /5 фг5т), Н5,„а = 2ааУ5 ([5а5т) И Т д. Таким образом, ряд кривой напряженности поля имеет следующий вид: h = 2ap/j (%Вт) sin mt — 2ap/3 ($vBm) sin 3«f -f- + 2aP/5(?pem)sin5(Bf-----f- -f- 2aa/j фага) COS cof — 2aa/3 ([5afim) COS 3u)f -f + 2ааУ5 фа#т) cos 5ш/ — . .. и состоит только из гармоник нечетного порядка. Как видим, гармонический состав напряженности поля весьма просто выражается через функции Бесселя соответствующих порядков. При этом реактивные слагающие напряженности поля определяются функциями Бесселя от мнимого аргумента, а активные — функциями Бесселя от действительного аргумента. Величины функций Бесселя до 11-го порядка для / и до 5-го порядка для / приведены в приложении П.7 и П.8. Более подробные таблицы функций Бесселя можно найти в «Математических таблицах» (т. 22, изд. АН СССР). Попутно без вывода дадим разложение в ряд Фурье периодических функций от гиперболического и кругового косинусов: 2/2 ch Вт sin at = /0 (Вт) -f 2 У (— 1 f2 Ih (Вт) cos Ь t, (3.44) ft=2 In cos Bm cos W = /0 (Bm) -f 2j£ (— 1)*/2 Л (Вт) cos Ы. 2. Определение среднеквадратичного значения напряженности поля и потерь в стали Разработанная модель дает возможность получить формулы для расчета среднеквадратичного значения напряженности поля Н и удельных потерь в стали Рсу. Для этого нужно воспользоваться известными соотношениями 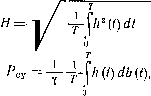 (3.45) где у — удельный вес стали. 86 Подставляя в (3.45) соответствующие выражения для hp(t) и ha(t), а также учитывая (3.44) и (3.44) и известные тригонометрические соотношения sh2;c = (ch 2х — 1), sin2j>c = -i- (1 — cos 2х), после интегрирования имеем я=у= V*l\hV№m)-[1 -Ш*вп)\, .(3.46) iJcy=Y-«afiW/i(Paflm)-(3-47) Подчеркнем, что полученные формулы являются более обобщенными, чем известные, например из [16]. Так, из (3.46), полагая аа = 0, можно получить формулу для среднеквадратичного значения Я = 1770(2р,Ям)-1,(3.46) широко используемую при расчетах цепей со сталью без учета гистерезиса. С другой стороны, из (3.47) вытекает, как частный случай, известная формула Штейнметца. Действительно, заменяя J\ рядом Тейлора су — ТГ- аат 1с klr(k + 2) и ограничиваясь учетом первого члена ряда, получаем выражение 1<0л. п2 2Т Введя обозначение р 1 ю о * су баз— 2 yc ааРа> получим формулу для потерь в стали, предложенную Штейнметцом, су-РсУбаз51,(3.47) где Рсубаз — удельные потери в сердечнике, вт[кг (5т= = 1 тл). Для дросселей с сердечниками, выполненными из стали Э310, обычно РсУ баз = 0,8 -г-1,3 вт[кг при / = 50 щ и ■Рсу баз = 7-т-12 еот/л:г при / = 400 гц. В заключение укажем, что формулы (3.46) и (3.47) дают результаты, хорошо согласующиеся с опытными данными. Точность расчетных формул повышается при аппроксимации кривых намагничивания соответственно двумя гиперболическими и двумя круговыми синусами. Пример 1. Требуется рассчитать магнитную характеристику H°=f(Bn) при синусоидальной магнитной индукции для идеального дросселя без зазора в магнитопроводе и построить ее в единичном масштабе. Кривая намагничивания аппроксимируется гиперболическим синусом с величиной В*баэ=13. Полный расчет величины Н° проведем для В°т = 10. Для всех других значений В°т приведем лишь готовые результаты. Среднеквадратичное значение напряженности поля определяется по формуле (3.46) н* = -yY K.(2<)-i = YT М2-10)- 1=4 670> где 1<,(2В°т) = /0 (2-10) = 4 356-10* (берется по табл. П.7). Результаты расчетов для всех значений В°т приведены в табл. 3.3. ТАБЛИЦА 3.3
 0 ... 11 12 13 14 15 16 17 |












