Раздел: Документация
0 ... 12 13 14 15 16 17 Приводя значения ВиЯк единичному масштабу (В*т=В°т/В*бг>2, Н* = H"/sh В*6аз), получаем значения В*т и Я*. Соответствующая расчетная кривая приведена на рис. 3.16,а (при k3—0). Пример 2. Требуется рассчитать магнитные характеристики H°km= f (m) и т = f (m) ПРИ синусоидальной магнитной индукции для идеального дросселя без зазора в магнитопроводе и построить их, в единичном масштабе. Кривая намагничивания аппроксимирована гиперболическим синусом с величиной В*ъйз = 13. Расчет величин lfkm и kT проведем лишь для Вдт= 8. Величины гармонических составляющих кривой напряженности поля при величине В°т= 8 находим по формулам .(3.44): Я°т=2Л (В°т) = 2/, (8) = 2-400 = 800, Я3°т=2/г«)=2/3(8) = 472,2, #5т=2ЧВт)=2М8)=171. где /h (В) — функция Бесселя; функция соответствующего порядка берется по табл. П.7. Коэффициент гармоник кривой напряженности поля при величине Вт=% равен Здесь 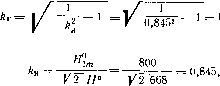 ,633. н°=wY° -1=уг v,°(2,8н=б68, где /о (16) =8934 • 102 — функция Бесселя нулевого порядка. Аналогичные расчеты проводятся для всех других значений Вт. Рассчитанные зависимости в единичном масштабе приведены на рис. 3.16,6 и е. Пример 3. Рассчитаем для идеализированного дросселя без зазора в магнитопроводе напряженность поля н гармонический состав кривой h(t) при значении В*т=\. Активная /га и реактивная Лр слагающие напряженности поля равны Ла = 12" 43& = 60,86, Лр = 0,0226 sh 6,44b. Определяем величину первой гармоники активной слагающей напряженности поля 60,8fl*mfl*6a3 60,8-1-13 " 1та~ ocpshB*6a30,0226-6,44 sh 13 0,0245 По выражению (3.46) при величине В*т = \ находим среднее квадратичное значение реактивной слагающей напряженности поля V/o (2 13)- 1 ■■ 0,398, V2 sh 13 по уравнениям (3.44) — гармонический состав кривой 2Л (13) Я*"Р= shl3 =°-419 2/3(13) Я*зтР= sh(13) —0,314, 2/5(13) Н smp =jg0,175, Н*ш = /(Я81в,)! +(Я*1тр)2 = l/"0,4192 + 0,0245== 0,4197. Среднее квадратичное значение напряженности поля при учете потерь в стали н* = V(H%y + (tf *1а)2 0,3982 + (у)2== °3984- Т А Б Л И Ц А 3.4
Коэффициент гармоник определим, пользуясь выражением где .Н\т 0,4.194 пг7лг kn = г—-=-т=-= 0,745. Y2 U* Y2 -0,3984 Далее можно найти кривую напряженности поля h(t) и ее активную Ла(0 и реактивную hp(t) слагающие. Результаты расчета сведены в табл. 3.4. 3.6. Аналитический расчет магнитных характеристик магнитопроводов идеальных и идеализированных дросселей с зазором При практических расчетах дросселей может появиться необходимость в определении следующих основных зависимостей: Ha=f(Bm, h), kTr=zf(Bm, ka), H, = f{Bm, kT), k3 = f(Bm, kT) и kaf(Bm, Яэ). Для получения таких зависимостей нами разработан специальный метод расчета, согласно которому магнитопро-вод с зазором заменяется «эквивалентным» сердечником без зазора [см. (3.2)], и расчет, в сущности, сводится к расчету, описанному в п. 2 этого параграфа. Напряженность поля эквивалентного сердечника Яэ может быть определена по выражению (3.14) с учетом формулы (3.46). Величину Яэ можно определить и несколько проще. Действительно, немагнитный зазор представляет собой при учете явления «выпучивания» или «уширения» потока линеаризированный элемент. Он не* вносит искажения в форму кривой тока дросселя, и, следовательно, напряженность магнитного поля эквивалентного сердечника может быть записана следующим образом: п h, = УТ(Н1М + kaHa)sinЫ + %\Г2 Я*стsinЫ. 3.5,... Как видим, напряженность магнитного поля эквивалентного сердечника отличается от напряженности поля сердечника без зазора (3.44) лишь по первой гармонике. Величины амплитуд высших гармоник кривой напряженности поля определяются только величиной Вт и не зависят от длины зазора, хотя их относительное содержание уменьшается за счет относительного увеличения первой гармоники. Принимая это во внимание, расчет напряженности поля в сердечнике с зазором можно произвести по формуле Яэ =/Я+2А.Я,Я1я + АХ.(3.48) 1. Расчет магнитных характеристик H3=f{Bm, k3) Этот расчет необходимо делать в следующем порядке. Для заданной величины Вт по формулам (3.44) и (3.46) с учетом (3.36) нужно определить средние квадратичные значения Яст и Я1ст. При определении Я° необходимо помнить о принятых масштабных коэффициентах аппроксимации: H°=—S-.(3.49) Далее по формуле (3.48) нужно определить искомую величину напряженности поля эквивалентного сердечника. Расчеты повторяют при других значениях Вт и ka. В результате можно получить искомые зависимости Яэ= = f(Bm, k3). Такие зависимости в единичном масштабе, полученные при аппроксимации кривой намагничивания гиперболическим синусом, приведены на рис. 3.16. Пример. Требуется рассчитать магнитные характеристики #э = f (Ерт, к3) при синусоидальной магнитной индукции для идеального дросселя с зазором в магнитопроводе и построить их в единичном масштабе. Кривая намагничивания аппроксимирована гиперболическим синусом (£*eas=13, а=0,0226 а/л, 0=6,44 1/гл). Расчет величины H°s проведем лишь для В°т = 10 и для немагнитного зазора ka = 1 • Ю-*. Среднеквадратичное значение напряженности поля = ]Л16702 + 2-Ы0 - 3-3,84.103.3770+(Ы0-3 • 3,86-107)2=4,24.10*. Здесь я°"=yr V1" (2<) -1=jr v°(20) 1=4 67°- н° — Я?ст=у2 /, = ]Л> Л (10) = 3 770, Я° = ш =- -™-= 3,86.10. У2 а„ }/"2.0,0226-6,44-4л.10-7 Рассчитанные магнитные характеристики в единичном масштабе приведены на рис. 3.16,а. 2. Расчет магнитных характеристик Hkm = f(Bm, ka) И kr = f(Bm, k3) Расчет может быть произведен подобно расчету характеристики для дросселя с магнитопроводом без зазора. Он должен отличаться только определением величины первой гармоники ННю + ЬН*.(3.50) Величина Я,ст не зависит от длины зазора и определяется по выражениям (3.36) и (3.44); величина Н3— по формуле (3.49) с учетом (3.36); высшие гармоники Hhm — непосредственно по формулам (3.36) и (3.44). При необходимости определения коэффициента гармоник следует воспользоваться формулой (1.2). Рассчитанные зависимости kr=f(B*m, k3) приведены на рис. 3.16,0. 3. Расчет магнитных характеристик B*m=f(H%, kT) и h=f{B*n, kT) Расчет 5*m=f(Я*э, kT) может быть произведен таким образом: задавшись Вт, по заданной напряженности #э по формуле (3.48) следует определить k з и затем коэффициент гармоник kT. 94 Задавшись k3, по заданному Вт следует определить #ст, На, # 1сТ и по ним — коэффициент kr. Рассчитанные кривые B*m=f(H*a, kT) при величине kr- = 5 и 15% приведены на рис. 3.16. Аналогичным путем можно получить зависимость k3=f(B*m, kr) (рис. 3.16,д). 4. Расчет магнитных характеристик k3=fiB*m, Н%) Задавшись £3, можно определить величину Яэ при определенном значении Вт по формуле (3.48). Рассчитанные кривые k3=f(B*m, Я*э) даны на рис. 3.16,г. При синусоидальном токе, протекающем по обмотке дросселя, кривая b(t) несинусоидальна. Несинусоидальна также и кривая b (t), ордината которой пропорцио-
Рис. 3.17. Формы кривых b(t) и b(t) при синусоидальном токе дросселя. нальна мгновенным значениям приложенного напряжения u(t) Подчеркнем, что формы кривых b (t) и b(t) в рассматриваемом случае имеют совершенно разный характер (рис. 3.17). Кривую b(t) и эквивалентную синусоиду кривой b(t) обычно оценивают максимальными значениями. Максимальное значение кривой b (t) будем обо- 0 ... 12 13 14 15 16 17 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||












