Раздел: Документация
0 ... 8 9 10 11 12 13 14 ... 17 кам может быть представлена в виде источников «регулируемых» э. д. с. с разомкнутой цепью; соответствующие ориентационные диаграммы приведены на рис. 3.9. Б. Параллельная схема замещения электрической цепи идеализированного дросселя. Эквивалентная комплексная проводимость обмотки идеализированного дросселя при переменном напряжении произвольной формы на его зажимах может быть представлена по каждой из гармоник в следующем виде: У =-{j- = y е ;<р = у cos? — jy sin f = g — jb, где g=gc, b=*bc — активная и соответственно реактивная проводимости идеализированного дросселя. Комплексы напряжения и тока по каждой из гармоник равны U = U, 1 = 1 е-/(р = / cos <р — /7 sin <р = /а —- /7Р. Как видим, при параллельной схеме замещения за основной вектор удобно взять вектор напряжения; ток при этом раскладывается на ортогональные составляющие. Схема замещения и векторная диаграмма, соответствующие данным уравнениям, приведены на рис. 3.7,6 и 3.8,6. Составляющая /а совпадает по фазе с напряжением и соответствует потерям в стали, а составляющая /р сдвинута по фазе относительно напряжения на 90° и характеризует реактивную составляющую индуктируемой э. д. с. Составляющие тока можно рассматривать как токи в соответствующих ветвях параллельной схемы замещения. При синусоидальном напряжении на зажимах рассматриваемого дросселя схема замещения его электрической цепи и соответствующая ей векторная диаграмма для основных гармоник имеют тот же вид, что и на рис. 3.7,6 и 3.8,6. По высшим гармоникам схема замещения может быть представлена в виде «регулируемых» источников тока с замкнутой цепью. Высшие гармоники тока при этом могут рассматриваться как результат действия источников, которое обусловливается синусоидальным напряжением и нелинейностью дросселя. Ориента-ционная диаграмма для этого случая приведена на рис. 3.9,а. 66 Следует подчеркнуть, что схемы рис. 3.7, а, б и соответствующие им векторные диаграммы справедливы и для дросселя с зазором в магнитопроводе, но в этом случае гс и х0 представляют собой уже эквивалентные активное и реактивное сопротивления магнитопровода с зазором. 2. Схемы замещения и векторные диаграммы магнитной цепи идеализированного дросселя Ввиду наличия связи между электрическими и магнитными величинами дросселя можно дать схемы замещения для его магнитной цепи. Намагничивающая сила (н. с.) при этом соответствует току: F = Iw,(3.27) а поток —напряжению: Ф = —[Оси = Л-.(3.28) Эти магнитные величины по каждой из гармоник как по величине, так и по фазе легко определяются через соответствующие входные величины напряжения и тока. Намагничивающая сила по каждой из гармоник совпадает при этом по фазе с током, а поток отстает от напряжения на угол в 90°. Поток Ф и намагничивающая сила F по каждой из гармоник связаны между собой законом Ома: F = Z Ф и Ф=У F,(3.29) г"И1 где и У — комплексные магнитные сопротивления и проводимости магнитной цепи дросселя. Величины F и Ф сдвинуты по фазе на угол а=£0, и, следовательно, их можно разложить на ортогональные составляющие, отличные от нуля. Для магнитной цепи идеализированного дросселя можно дать две схемы замещения. Последовательная схема замещения отображается первым уравнением; па« 5*67 раллельная — вторым. Такие схемы приведены на рис. 3.7,в и г. А. Параллельная схема магнитной цепи идеализированного дросселя без зазора в магнитопроводе. По величинам F. и Ф, рассчитанным по уравнениям (3.27) и (3.28), можно определить параметры схемы замещения магнитной цепи идеализированного дросселя. При питании последнего напряжением произвольной формы имеем Y =— = и е~~1л = и cos а — /« sin а = b — /V , F—F, Ф—Ф e~a =■ Ф cos а — /Ф sin а — Фр — /Фа. Схема замещения и векторная диаграмма, соответствующие этим уравнениям, приведены на рис. 3.7,8 и 3.8,в. В схеме источник н. с. изображен в соответствии с физикой процессов, протекающих в дросселе {70]. В векторной диаграмме рис. 3.8,е вектор н. с. совмещен с осью действительных величин. Магнитный поток разложен на составляющие. Первая составляющая Фр совпадает по фазе с н. с. и представляет собой реактивную составляющую потока, а вторая Фа — активную составляющую. Последняя осуществляет передачу энергии в сталь сердечника, где она преобразуется в тепловую. Действие этой составляющей вызывает в электрической цепи появление э. д. с, совпадающей по фазе с током, которая и соответствует для данной гармоники величине потерь в обмотке, вносимых сердечником. Реактивная составляющая потока наводит в электрической цепи э. д. с, сдвинутую по фазе относительно тока на 90°, которая определяет индуктивность дросселя по данной гармонике. Заметим, что в отличие от принятого обозначения комплексов электрических величин здесь мнимой частью комплексного числа отражается активный процесс, а вещественной— реактивный процесс. Это сделано для упрощения согласования между собой электрических и магнитных величин, так как из выражения (3.28) видно, что напряжение и поток связаны между собой величиной /, Б. Последовательная схема замещения магнитной цепи идеализированного дросселя без зазора в магнито-68 проводе. Параметры последовательной схемы замещения магнитной цепи по каждой из гармоник равны z»=р~ф = \ еа = \cos <+ sn * = \+/ V Для этой схемы в качестве исходной величины принят поток, и поэтому имеем Ф = Ф, F = f;e/a = F cos a + jF sin a = Fp +rjF* Схема замещения для этого случая приведена на рис. 3.7,г; векторная диаграмма — на рис. 3.8,г; направление вектора потока совмещено с осью вещественных величин. На этой схеме н. с. представлена состоящей из двух слагающих, из которых Fv совпадает по фазе с потоком и является реактивной составляющей, а F& сдвинута по фазе относительно потока на 90° и является активной составляющей. Параметры магнитной цепи дросселя имеют вполне определенную связь с параметрами его электрической цепи: gc bD=X-(3-3°) cote Как видим, сопротивления электрической цепи дросселя пропорциональны магнитным проводимостям сердечника, а ее проводимости— соответствующим магнит-< ным сопротивлениям. Эти связи позволяют по параметрам магнитной цепи определить параметры электрической цепи и наоборот. Схемы замещения — последовательная и параллельная — однозначно характеризуют дроссель и дают одинаковые результаты. Однако следует отметить, что при синусоидальном напряжении на зажимах дроссель лучше характеризовать параллельной схемой для электрической цепи и последовательной для магнитной, а при питании синусоидальным током — последовательной схемой для электрической цепи и параллельной для магнитной. Из сопоставления всех схем замещения и векторных Диаграмм можно заметить, что последовательной схеме замещения электрической цепи соответствует параллельная схема замещения магнитной цепи и, наоборот, параллельной схеме замещения электрической цепи соответствует последовательная схема магнитной цепи. Векторная диаграмма потоков, построенная по параметрам магнитной цепи, идентична векторной диаграмме напряжений, построенной по параметрам электрической 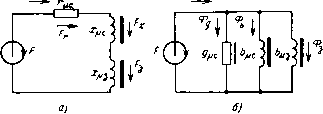 Рис. ЗЛО. Схемы замещения магнитной цепи дросселя с зазором: а — последовательная; б — параллельная. цепи, причем положение их фиксировано — потоки отстают от соответствующих напряжений на 90°. Векторные диаграммы токов и н. с. подобны. Комплексы магнитных величин М следует изображать через угол потерь M = Me±ia-(3.31) Знак плюс берется тогда, когда за основной вектор принимается поток, а минус, когда принимается н. с. В. Схемы замещения магнитной цепи идеализированного дросселя с зазором в магнитопроводе. Схему замещения магнитной цепи идеализированного дросселя и соответствующую ей векторную диаграмму можно получить и для идеализированного дросселя с зазором в магнитопроводе по электрическим величинам — току и напряжению. На рис. 3.10,а приведена для общего случая последовательная схема замещения магнитной цепи дросселя с зазором. Векторная диаграмма для нее дана на рис. 3.11,а; напряжение на диаграмме совмещено с осью мнимых величин. Параллельная схема замещения магнитной цепи дросселя с зазором приведена так-70
ОС, FX а) <Р *1
в) Рис. 3.11. Векторные диаграммы дросселя с зазором в магнитопроводе: а — для последовательной схемы; б — для параллельной схемы. же для общего случая на рис. 3.10,6; соответствующая ей векторная диаграмма —на рис. 3.11,6. 3.4. Аппроксимация кривых намагничивания ферромагнитных сердечников. Относительные единицы. Определение коэффициентов аппроксимации Для теоретического анализа свойств дросселя нужно иметь аналитические выражения, отображающие свойства его ферромагнитного сердечника. Эти свойства зависят от многих факторов. Поэтому задачу по определению аналитических выражений целесообразно разбить на две отдельные самостоятельные задачи. В первой определим выражение, отображающее свойства сердечников при режиме квазистатичеокого намагничивания; во второй учтем влияние изменения этих свойств при режиме динамического намагничивания. В этом параграфе рассмотрим первую задачу, вторую — в § 3.5. Свойства ферромагнитного сердечника при квазистатическом режиме намагничивания (d-ty/dt—>-0) в полной мере характеризуются семейством статических (квазистатических) петель гистерезиса. Очевидчо, описав эти свойства аналитически, получим возможность выполнять расчеты дросселей аналитическими методами. 0 ... 8 9 10 11 12 13 14 ... 17 |
||||||||||||||||||||||












