Раздел: Документация

0 ... 6 7 8 9 10 11 12 ... 17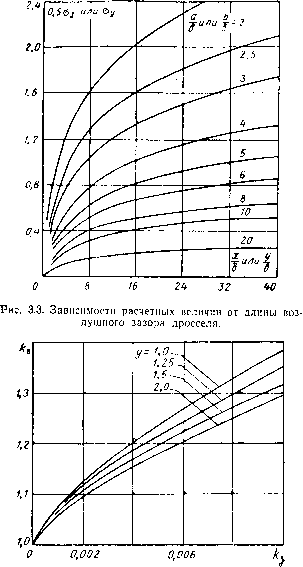

Рис. 3.4. Зависимости коэффициента «выпучивания» от длины зазора и относительной высоты магнитопровода, выполненного по НО.666.002.

Замена идеального или идеализированного дросселя с зазором эквивалентным дросселем с полностью замкнутым магнитопроводом позволяет использовать те же взаимосвязи для электрических и магнитных величин, что и для дросселя, рассмотренного в п. 1 этого параграфа.

3. Реальный дроссель

Связи между электрическими и магнитными величинами в этом случае можно получить с помощью комплексного метода [64]. В соответствии с этим методом все связи устанавливаются не по мгновенным значениям, а по средним или действующим значениям-изображениям по k-м гармоникам. При этом любая периодическая величина, симметричная относительно оси абсцисс, представляется в виде тригонометрического ряда

п

/(*)= Yi ftmsin(br-fW

*=1, 3, 5...

или в комплексной форме записи

/(*)=МЧ £ Актеш,

А = 1, 3, 5

где

г

и

носит название комплексной амплитуды по k-й гармонике.

Анализ процессов, протекающих в дросселе, упрощается при введении понятия о комплексной индуктивности [64]. Ее можно получить из выражения

Ф = /-(»)»,(3-18)

где L(i)—мгновенная индуктивность дросселя.

Периодически изменяющиеся потокосцепление и ток изображаются тригонометрическими рядами с соответствующими комплексными амплитудами. Формы кривых г5(/) и /(f) различны, и поэтому связь между ними можно определять лишь по соответствующим гармоникам.

55

---

В результате комплексный коэффициент связи по k-k гармонике между потоком и током, представляющий собой индуктивность дросселя, можно записать в виде

г

-у- j" L (О I dt Lk=—Ц-.(3.19)

у- [i(t)z-,kmtdt

О

Комплексную индуктивность характеризуют не только по модулю, но и по фазе:

Lk = Lke~!\(3.20)

где afe — угол, сдвига фаз между магнитной индукцией и намагничивающей силой дросселя по k-й гармонике.

Выражение (3.19) позволяет учесть влияние на k-ю гармонику тока других гармоник, гистерезиса, вихревых токов и пр.

При использовании понятия комплексной индуктивности Zh ток с напряжением связан следующим соотношением:

jhm=-- ,(3.21)

г + jki£>Ls + jk(aLh

где Ukm и /ftm — комплексные амплитуды напряжения и тока по k-й гармонике.

Расчет электрического режима дросселя методом комплексного исчисления громоздок. Практически более удобен метод гармонического баланса. Его можно применять для расчета дросселя с относительно малой нелинейностью, например для дросселя с зазором в маг-нитопроводе или для дросселя, работающего в режиме, близком к синусоидальному.

Сущность метода гармонического баланса состоит в линеаризации. По этому методу нелинейный дроссель заменяется линейным, причем так, чтобы амплитуды напряжения или тока линейного дросселя были равными амплитудам основных гармоник напряжения или тока нелинейного дросселя.

56

Индуктивность линеаризированного элемента можно получить из (3.19). При синусоидальном напряжении, а следовательно, потоке

L =----;(3.19)

/2

Т

■i(t)trlatdt

при синусоидальном токе

7

L (()( е~ы dt

(3.19")

При синусоидальном напряжении комплексные индуктивности по высшим гармоникам равны нулю и, следовательно, дроссель работает в режиме генератора высших гармоник тока. Напротив, при синусоидальном токе комплексные индуктивности по k-м гармоникам стремятся к бесконечности, т. е. при таком режиме дроссель работает в режиме источника высших гармоник э. д. с.

Закон Ома при использовании эквивалентных линейных параметров для цепи дросселя (рис. 3.1) имеет следующий вид:

7= , . Л ■ f •(З-21J

Подчеркнем, что величина индуктивности, определенная по выражению (3.19), т. е. при синусоидальном напряжении, не равна величине индуктивности, определенной по формуле (3.19"), т. е. для дросселя при синусоидальном токе. При расчетах цепей с линейными дросселями следует учитывать это обстоятельство и применять то или иное выражение для индуктивности исходя из конкретного режима работы дросселя.

Наконец, связи между напряжением и током для реального дросселя можно установить по методу эквивалентных синусоид. При этом считают, что амплитуда эквивалентной синусоиды равна действующему значению соответствующей несинусоидальной величины, умноженной на/ 2, а сдвиг фаз между эквивалентными сину-

---

Сойдами напряжения й тока определяется формулой

<? = arccosJ.(3.22)

Подчеркнем, что метод эквивалентных синусоид практически можно использовать только в случае, когда одна из величин дросселя (напряжение или ток) синусоидальна.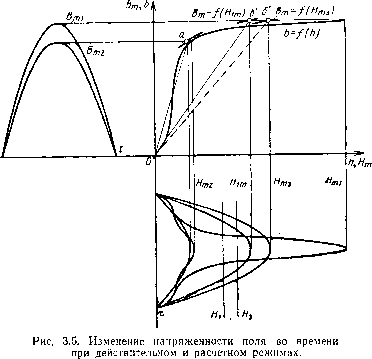

Линеаризацию дросселя по методу гармонического баланса и эквивалентных синусоид лучше всего проиллюстрировать графически. Для дросселя с Малыми потерями и различными по величине синусоидальными на« пряжениями на его зажимах форма кривой тока и, следовательно, напряженности поля качественно обусловливается в эквивалентном процессе уже не «кривой

намагничивания [формула (3.3)], а серией прямых, проходящих через начало координат. При каждом значении напряжения на дросселе наклон прямой определяется максимальными значениями магнитной индукции и эквивалентной напряженности поля. Эквивалентная напряженность магнитного поля по методу гармонического баланса определяется по первой гармонике тока, а по методу эквивалентных синусоид — действующим значением тока, протекающего по обмотке:

или

#m3= К2 Я.

На рис. 3.5 приведены кривые изменения напряженности поля в зависимости от времени для действительного и расчетного режимов. На этом рисунке b = f(h) — кривая намагничивания, характеризующая изменение магнитного состояния в реальном сердечнике идеального дросселя; оа и об— прямые расчетных частных циклов, характеризующие изменение магнитного состояния в эквивалентном сердечнике соответственно при величинах В mi и Вт2; Bm=f(Hm) и Bm=f(Hna) — расчетные кривые намагничивания эквивалентного сердечника (геометрическое место вершин частных расчетных циклов).

Для дросселя с потерями введение эквивалентной синусоиды равносильно замене действительной петли гистерезиса эквивалентной эллиптической петлей [4] (рис. 3.6), площадь которой в некотором масштабе выражает потери на гистерезис, вихревые токи и пр. Замена реальной петли гистерезиса эквивалентным эллипсом дает возможность применять для инженерного расчета и для исследования дросселей теорию синусоидальных переменных токов и, в частности, строить векторные диаграммы. При этом расчет нелинейного дросселя или вообще цепи с ним по существу не отличается от расчета дросселя с линейными свойствами. Отличие заключается лишь в том, что расчет приходится делать не один раз, а с итерациями.

Энергетические соотношения в реальном дросселе можно получить, исходя из следующих соображений.

0 ... 6 7 8 9 10 11 12 ... 17