Раздел: Документация
0 ... 123 124 125 126 127 128 129 ... 143
Рис. 11.28. Семейство фазовых характеристик объекта. Знак управляющего воздействия Um может изменяться не более одного раза. Запишем уравнение (11.59) с учетом знака Um: В = в0-Т(у~у0)± TkUm In I у ± Wm J Т TkUm In I у„ ± «/m . (11.60) Обозначив a = ±1, запишем уравнение (11.60) 0 = в0 — Т(у — у0) + оТШт\п у + akUm\- - oTkUm ln\y0 + akUm I.(11.61) Подставив в уравнение начальное значение производной у0 = = abjdt = 0, получим 6 = 60 — Ту + oTkUm\п\у + akUm — аТШпInakUm. (11.62) На основании уравнения (11.62) строятся фазовые траектории в плоскости 0, у. Пусть Т = 0,62 с, k = 0,023 рад/Вс, ит = 220 В, 00 = —0,5 рад. Подставим численные значения коэффициентов в уравнение (11.62)j е = —0,5 — 0,62# + о -0,311л# + а-0,5 — а -0,311па0,5. (11.63) Для первого участка траектории a = —1 и уравнение (11.63) примет вид 0 = — 0,5 — 0,62# — 0,311п — 0,51 -f- 0,31 lxi — 0,51. (11.64) В соответствии с уравнением (11.64) на рис. 11.28 построена фазовая траектория АВ. Она проходит через точку 0 = 0О = —0,5; у =* = Уо — 0. Семейство фазовых характеристик, соответствующих а = = —1 при других начальных значениях, на рисунке обозначено цифрой 1, а семейство характеристик, соответствующих о= 1,— цифрой 2. В соответствии с фазовой траекторией АВ ошибка системы от значения 80 = —0,5; Уо = 0 уменьшается. Однако, если не изменить знака а управляющего воздействия, то 0 пройдет через нулевое значение с некоторой скоростью у и будет возрастать до бесконечности со скоростью у = 0,5 рад/с. Для устранения ошибки изображающая точка должна попасть в начало координат 0 = 0, у = 0, т. е. должна с фазовой траектории АВ (или любой другой траектории) «перейти» на фазовую траекторию, проходящую через начало координат (направление движения изображающей точки указано стрелками). Уравнение последней получим, подставив в уравнение (11.62) 0О = 0: 0 = Ту + оТШт\п\у + okUm — аТШтInakUm, (11.65) или после подстановки значений коэффициентов в = — 0,62 + о • 0,31 In у + а ■ 0,51 — о . 0,31 In 0,5. (11.66) Уравнению (11.66) соответствует фазовая траектория M0N. Эта траектория является единственной, по которой можно попасть в начало координат. Как отмечалось, в точках пересечения фазовых траекторий с траекторией M0N изображающая точка должна переходить с этих фазовых траекторий на траекторию M0N. Такой переход достигается переключением знака управляющего воздействия. В связи с этим траекторию M0N называют линией переключения. Если в начальный момент е0 = —0,5, у = 0, то в результате подачи управляющего воздействия и = —0т (а = —1) изображающая точка пройдет путь тп; в точке п пересечения с траекторией MCN необходимо переключить знак и. Под влиянием и = + Um (с = + 1) изображающая точка пройдет по траектории MCN путь пО, т. е. пе- * реместится в начало координат. В общем случае, когда в начальный момент значение у = abldt Ф 0, т. е. двигатель вращается, фазовая траектория может начинаться с любой точки фазового пространства * (например, в точках /х, /2) и оптимальная траектория также будет состоять из двух отрезков кривых (liti и пО; 12п и пО). В частном слу--. чае, когда в начальный момент изображающая точка находится на линии переключения M0N, оптимальный процесс управления будет со-стоять из одного интервала. Для определения оптимального закона управления (функции переключения), зависящего от 0, у, kUm, используем линию переключения. Перепишем уравнение (11.65) линии переключения в виде 0+ Ту—oTWm \п\у + okUm + оТШт In аШт = 0, или, учитывая, что о = —sign у (фазовые траектории 1, соответствующие знаку а = —1, пересекают траекторию M0N при положительных значениях у и наоборот), 0 + Ту + (sign у) TkUm \п\у — (sign у) Шт — — (sign у) TkUm In I kUm I = 0.(11.67) Из приведенных выше рассуждений следует, что если изображающая точка находится ниже линии переключения M0N (левая часть уравнения (11.67) отрицательна) или на участке ON, то управляющее воздействие должно быть отрицательным (и = —Um), если же она находится выше этой линии (левая часть уравнения (11.67) положительна) или лежит на ее участке МО, то управляющее воздействие должно быть положительным (и = -Ь/т)- Поэтому оптимальный за- кон управления (функция переключения управляющего воздействия) будет иметь вид: « = c/msign[8+7VH- + (sign у) ТШт In у —. (sign у) х X Шт - (sign у) TkUm In Шт I), (11.68) или 4 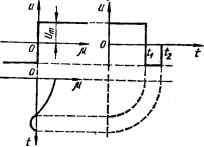 M = [/msign в + Ту + Рис. 11.29. Реализация функции ы = = (sign u) £Ут с помощью идеального двухпозиционного реле. + (signy)TkUm\n у — (sign у) kU, — ] . (11.69) хюсле подстановки численных значений коэффициентов получим и = Um sign [б + 0,62у + (sign у) 0,31 In У~(5У °5 ] , (П .70) т. е. полярность управляющего воздействия (напряжения Um) и моменты его переключения при Um = const зависят от ошибки системы 6 и ее производной у = dbldt. Поскольку для определения ошибки необходимо управляемую величину хх (см. рис. 11.15) подавать на элемент сравнения ЭС, то оптимальный закон управления (11.70) может быть реализован в замкнутых системах автоматического управления (см. рис. 11.26). Обозначив выражение в квадратных скобках через р,, перепишем формулу (11.70) в виде M = (signLi)c/m,(11.71) откуда следует, что на управляемый объект УО должно подаваться максимальное напряжение Um, знак (sign) которого соответствует эс г- W-х- ; г->Ф d 7t OJSZy 1 . 1*№У)0,5 Т 0,31 у-(«дпу)0,5 0,5 га Рис. 11.30. Структурная схема оптимальной по быстродействию замкнутой системы автоматического управления. 0 ... 123 124 125 126 127 128 129 ... 143
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
