Раздел: Документация
0 ... 121 122 123 124 125 126 127 ... 143 получаем! XiK = Azo -f- А21 -4- Л22; где Л 20 = —kUm, откуда находим постоянные интегрирования: Л22 — Pi Pi —Pi. (xlK + Wm)- Л«1 — — ■ Pi — Рг (*1к + Шт)+. Pi — Рг + Чк Pi —Pi 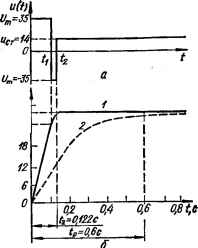 X(P{ 30 Xi,r28 Подставив полученные значе-„ no ллJ/11 ип"ис- 11-22- Оптимальный закон изме- ния. ли и л22 в уравнениенения управляющего воздействия (а)к получим решение на втором интер-кривые переходного процесса (б), вале управления: * (0 — Я/я + [-(х1к + «/„) + --] ем + + кле* - р2е*0 (*1к + Шт) + х1к («*• - е*0] - , (11.53) или после подстановки конкретных значений х1к, х\к и других величин x(f) = — 70 + [(— 10е-15-15 + 15е-10) (25,162 + 70) + + 306,598 (е-10 — е-15-15)] (— 0,2). Второй интервал очень мал (Аг = t2 — tt = 0,122—0,1054 = = 0,0166 с), поэтому можно определить х (t) только для одного конечного момента времени t = 0,0166 с: x(i) = — 70 + [(— lOe-15-15 0-0166 + 15е-1000166) 95,162 + -+-306,598 (е-10-о*0166 — е—15-15 0-0166)] (— 0,2) = 28 ед. Закон изменения оптимального управляющего воздействия и (f) и переходный процесс х (/) представлены на рис. 11.22, а, б (кривая /) соответственно. Значение управляющего воздействия и (t), которое должно быть подано скачком на вход объекта в момент ts окончания переходного процесса для поддержания достигнутого значения х (t) = х2к, равно «ст = ХйД = 28/2 = 14 ед. Таблица 11.3. К расчету переходного процесса
С целью сравнения рассчитаем переходной процесс и найдем время переходного процесса для случая, когда на вход управляемого объекта (см. рис. 11.19, а) подается не оптимальное управляющее воздействие (рис. 11.22, а), а ыст = 14, соответствующее установившемуся значению выходной величины х2к = 28 ед. Переходный процесс в этом случае будет определяться формулой, аналогичной формуле (11.45): х®=А10 + А11е»*< + А12еъ*, где А10 = kuCT; АХ1 = kupj{px — р2); Ам = —kuCTpx/(px—p2), т. е. Ахх и находятся по формулам, аналогичным (11.48). Подставив значения постоянных времени в выражение для х (t), получим х® = (1 + —£—ел*--&—&Л kuCT, или после подстановки численных значений параметров x(t) - (1 — 3e-iw + 2е-15-150 • 28. Рассчитанные значения х (t) для различных t приведены в табл. 11.3. Кривая переходного процесса, построенная по данным табл. 11.3, изображена на рис. 11.22, б (кривая 2). Из рисунка видно, что время переходного процесса tp = 0,6 с, т. е. оно в tvlt% = 0,6/0,122 « 5 раз больше, чем в системе, оптимальной по быстродействию. Оптимальные по быстродействию разомкнутые САУ Оптимальное по быстродействию управляющее воздействие и вырабатывается с помощью управляющего устройства У У (рис. 11.23, а). Согласно теореме об п интервалах управляющее воздействие во время переходного процесса принимает только два значения: и — +0т и и = —Um. Для переключения полярности управляющего воздействия обычно используется релейный элемент РЭ (рис. 11.23, а), характеристика которого (рис. 11.23, б) описывается выражением: Um, если р. > 0; — Um, если р. < 0; 0, если у, = 0. £- PS
УУ
Память. Функция Рис. 11.23. Функциональная схема оптимальной по быстродействию разомкнутой системы управления (а) и статическая характеристика релейного элемента (б). Вы fop знака первого интервала Определения tf,t,...,tn Проверка цифровых ветчин в непрерывные Рис. 11.24. Блок-схема расчетов моментов переключения. Рис. 11,25. Функциональная схема оптимальной по быстродействию программной разомкнутой системы управления. Сигнал р, подаваемый на релейный элемент, должен изменять свою полярность в соответствующие моменты времени tt. Моменты переключения tt можно определять в соответствии с рассмотренной выше методикой на основе заданных начальных и конечных условий или используя фазовые координаты объекта .(рис. 11.17—11.20). При формировании оптимального управляющего воздействия на основе заданных граничных условий оптимальное управление реализуется в разомкнутых системах (рис. 11.23, а). В таких системах выходная величина объекта и ее производные не подаются на УУ и не используются для формирования управляющего воздействия. В оптимальных по быстродействию разомкнутых системах управления для определения моментов переключения tt прибегают к цифровым вычислительным устройствам ВУ, с помощью которых решаются системы трансцендентных уравнений типа (11.49). Расчеты моментов переключения tt выполняются в соответствии с алгоритмом вычислений, одна из которых изображена на рис. 11.24 [48]. Как отмечалось, в разомкнутых системах моменты переключения рассчитываются в зависимости от векторов состояния управляемой величины в начальной хн и в конечной хк точках фазовой траектории. Поэтому, если начальные и конечные условия остаются одинаковыми 0 ... 121 122 123 124 125 126 127 ... 143 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||












