Раздел: Документация
0 ... 119 120 121 122 123 124 125 ... 143 ющими промежуточными ограничениями по величине переменными. Пусть, например, имеем объект второго порядка (см. рис. 11.19, а) и кроме задающего воздействия и ограничена еще промежуточная переменная их значением max (рис. 11.20). Чтобы не превысила допустимого значения U\ max. в момент tx и уменьшается от Umax ДО U = Ui max/*l И ЗНЭЧеНИе и ПОД- держивается до очередного момента t2 изменения знака и. После этого их начнет изменяться в другом направлении. Таким образом, создается новый интервал управления tt —t2 с пониженным значением управляющего воздействия на вхо объекта, вследствие чего длительность переходного процесса увеличивается по сравнению с отсутствием ограничения щ. Как видно из рис. 11.20, число интервалов управления в рассматриваемом случае k = 3, что соответствует также значению ft, полученному с помощью формулы (11.32): 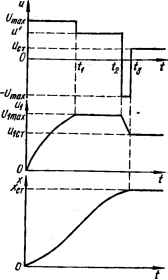 Рис. 11.20. Пример оптимального по быстродействию управления объектом второго порядка> при ограничении ы и щ. k = (2— 1 + 1)(1 — 0 + 1) —1 = 3. Теорема об п интервалах значительно облегчает нахождение оптимального управляющего воздействия, так как она исключает необходимость определения функций % и их анализа. Если характеристическое уравнение управляемого объекта содержит комплексные корни, то число переключений в зависимости от начальных условий может быть любым, поэтому теорема об п интервалах в этом случае не может быть использована [75]. С помощью оптимального по быстродействию управления возможно решение задачи не только быстрейшей отработки задания, но и устранения за минимальное время отклонения управляемой величины объекта, вызванного возмущающими воздействиями. Определение моментов переключения управляющего воздействия при оптимальном по быстродействию управлении линейными объектами В соответствии с теоремой об п интервалах оптимальное по быстродействию управление объектом n-порядка с отрицательными вещественными или нулевыми корнями характеристического уравнения состоит из п интервалов, в каждом из которых управляющее воздействие- принимает свое предельное значение Um, а знаки этого воздействия в конце интервалов переключаются. Для технической реализации управляющего устройства, с помощью которого вырабатывается оптимальное по быстродействию управляющее воздействие и, необходимо знать предельное значение этого воздействия Um и п моментов (включая момент окончания управления) переключения 11г t2, tn. Предельное значение Um определяется с учетом предельно допустимых эксплуатационных режимов управляемого объекта. Более сложной задачей является определение моментов переключения управляющего воздействия, которые зависят от многих факторов: параметров объекта (постоянных времени, коэффициента усиления и др.), от вектора состояния в начальной хн и конечной хк точках фазовой траектории, допустимого предельного управляющего воздействия Um, от вектора возмущающих воздействий L. Для упрощения этой задачи будем искать моменты переключения как функции хн и хк при отсутствии возмущающих воздействий и неизменных параметрах системы. Пусть управляемый объект описывается дифференциальным уравнением л-го порядка c„- + Cn-iS-+ ••• +с0х = Шт.(11.33) Считаем, что корни характеристического уравнения с„р" + -+- cn ip"- + ... + с0 = 0 вещественные отрицательные и некратные. Начальное состояние объекта при t = О характеризуется вектором хн = (х0, х0, ХсГ-конечное при t = tK вектором хк = (х„, х„, х("—Требуется за минимальное время перевести вектор состояния из хн в хк. Как известно, для этого нужно п интервалов управления. На интервалах управления и \ = Um, а знаки чередуются (п — 1) раз, следовательно, требуется определить п моментов переключения, включая время окончания управления. Для определения моментов переключения воспользуемся методом стыкования решений дифференциальных уравнений со знакопеременной правой частью [48]. Решение уравнения (11.33) имеет вид *(9 = Лв + Л1е* + Л.е«+ +Л„еЧ(11.34) где pi — i-й корень характеристического уравнения; А{ — i-я постоянная интегрирования — начальное значение i-й компоненты переходного процесса. Так как в начале каждого интервала скачком изменяется управляющее воздействие, то и значения А0, Аъ ... , Ап также будут изменяться скачком при переходе от одного интервала к другому. Для решения поставленной задачи необходимо предварительно найти значения постоянных интегрирования на каждом интервале управления. Сперва определим постоянные интегрирования А„\, Ап2, ... * Впредь для простоты записи предельное значение управляющего воздействия вместо fmax будем обозначать Um. Ann Для последнего л-го интервала управления. Отметим, что в конце /1-го интервала управления при t = tn заканчивается процесс и вектор управляемой величины х (/„) равен заданному конечному значению х (tn) = хк = {хп, хп, .... хп~1). Записав решение (11.34) для управляемой величины и ее (л — 1) производных в момент tn и приравняв им соответствующие координаты вектора хк, получим систему из л уравнений: Л„,ер« + Ап2ер1п + ... +Аппеп = Хп±Шп ptAnlehtn+ p2/W*»+ +рпАппе"пп = Хп \ (11.35) pf-nAratn + ft-l)AnSn+ ... +рГ1)Апперп{п = х-1), j где Апо = ±kUm- Из системы уравнений (11.35) определяются постоянные интегрирования Апи Anz, Апп на п-м интервале управление . поскольку все координаты управляемой величины непрерывны, возможно отыскание решений на границе последнего и предпоследнего интервалов: (Л(„ ш - Ащ) е"-1 + (Л<„ 1)2 - Л„2) ер-1 + • • • ... + (Л(„ 1)п — Апп) е"»""1 = Т 2Um; рх (А1п и1 — Ап1) е"1"-1 + р2 (iV-и — Ani) е"*»-1 + • • . ■ • • +Рп (А{п-т — Апп) е""-1 = 0; (11.36) рТ~1) (Л(„ ш - Дч) ер,п- + pf~l) (Л(„ 1)2 A*) ер»- + • • • + РГ" (m-i,n - Ат) ep«n-i = 0. Из системы уравнений (11.36) определяют (A(n—i)i — Ani), i — 1, 2, л. Подставляя ранее найденные значения Л„,- в (11.36), определяют Ain-i)i- Продолжая аналогичные стыкования решений на последующих интервалах вплоть до первого, исключают постоянные интегрирования на промежуточных интервалах. Значения Аи для первого интервала определяют с учетом начальных условий при t = 0 из следующей системы уравнений: А1 + А2 + ••• + Ащ = х0 ±kUm; Р1А11 + раАц+ ••• +р„Аы = х0; Р1Г1)Аг1 + рГ %2 + . • • + рАгп = xf~\ (11.37) В результате такого исключения постоянных интегрирования получается система из л транцендентных уравнений с п неизвестными 0 ... 119 120 121 122 123 124 125 ... 143 |












