Раздел: Документация
0 ... 118 119 120 121 122 123 124 ... 143 Рис. 11.18. Пример оптимального по быстродействию управления объектом, представляемым интегрирующим звеном.
Таким образом, если объект описывается уравнением первого порядка, то процесс управления в оптимальном по быстродействию переходном режиме состоит из одного интервала 0 — tt. Рассмотрим два апериодических звена, соединенных последовательно (рис. Il.l9, а), управляющее воздействие и ограничено значением сУтах. Такое соединение звеньев может представлять собой математическую модель электромашинного усилителя мощности (ЭМУ), модель двигателя постоянного тока, когда за выходную величину х принимается угловая частота со его ротора и др. Для возможно быстрого изменения х (разгона двигателя) от х (0) = = 0 до Хст следует, очевидно, на вход второго звена, как и в случае одного апериодического звена (см. рис. 11.17), подать скачком максимальный по своему значению сигнал щт. Однако сигнал ых снимается с выхода первого апериодического звена, поэтому вследствие инерционности этого звена их не может быть изменен скачком от 0 до щт. Чтобы сигнал ых был предельно близок по форме к оптимальному управляющему сигналу, на вход первого звена следует подавать скачком сУпих, что обеспечивает максимально быстрый рост иг в направленное-его предельного значения щт (рис. 11.19, б)§ При достижении х — хст сигнал иг следо*; вало бы скачком уменьшить до значения «1ст = x„/k2, соответствующего требуемой установившейся величине хст. Однако изменить ых скачком нельзя из-за инерционности первого звена. Для возможно быстрого уменьшения ut до «iCT необходимо управляющее воздействие и предварительно, в момент времени tlt когда х еще не достигло значения хст, переключить с + -+- tVmax на — сУщах и сохранить это значе-Рис 11.19. Пример оптималь- ние до момента t2, пока их не снизится от ного по быстродействиюзначения и\ в момент L до значения «iCT управления объектом, пред-1D „ „ ставляемым двумя апериоди-и * не Достигнет величины хсх. В момент ческими звеньями.времени /а следует и мгновенно изме- 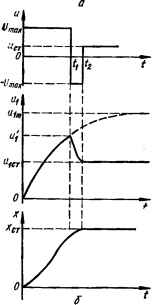 нить до ыСт = U\crlkv На этом переходный процесс заканчивается. Таким образом, для достижения оптимального по быстродействию переходного процесса последовательного соединения двух звеньев первого порядка с вещественными отрицательными корнями характеристического уравнения (р, = —1/Гх; р2 = —1/Г2) процесс управления должен состоять из двух интервалов, в каждом из которых управляющее воздействие и принимает одно из двух своих предельных значений ± Umax- на первом интервале 0 — ttu = + (7max, на втором интервале — t2 и = —(У max- Знак и в первом интервале совпадает со знаком конечного значения ыСт- Аналогично можно показать, что в общем случае для достижения оптимальности по быстродействию п последовательно соединенных линейных звеньев первого порядка, или линейного объекта «-го порядка, с вещественными отрицательными или нулевыми корнями характеристического уравнения при наличии ограничения управляю-шд: воздействия процесс управления должен состоять из п интервалов, в каждом из которых управляющее воздействие принимает свое предельное значение, т. е. закон оптимального управления является релейным. В конце каждого интервала происходит переключение знака управляющего воздействия. Знак и в первом интервале определяется направлением изменения управляемой величины х. При ненулевых начальных условиях число интервалов управления может быть меньше п. Действительно, если, например, в момент начала процесса управления значения управляемой величины х и ее производных оказались такими, как в конце k-ro интервала управления для случая нулевых начальных условий, то процесс управления будет состоять только из (п — k) интервалов. Приведенное положение о числе интервалов управления носит название теоремы об п интервалах. Она была впервые сформулирована и доказана А. А. Фельдбаумом в 1949 г. [75]. Докажем теорему об п интервалах с помощью принципа максимума Понтрягина. Пусть объект описывается системой уравнений dxjdt = ф,(х1, х2.....хп)-\-Ьси, 1 = 1, 2.....п, (11.24) или в векторной форме dx/dt = ф (х) + Ьи,(11.25) где и — управляющее воздействие; х (xlt х2, х„), ф (ц>и ф2, .... ф„), b Фъ b2, bn) — соответствующие векторы. Функции ф,- считаем дифференцируемыми. Управляющее воздействие ограничено по величине U = (Ушах- Согласно формуле (11.10) и учитывая, что dxldt = ф (х) + bu = V, гамильтониан Н = = ф [ф (х) -f- bu) = •фф (и) + -фи.(11.26) Так как от управляющего воздействия и зависит только второе слагаемое, то с учетом ограничения на и максимум Н будет при п « = i7maxSigntoj> = signE b,(11.27) т. е. оптимальное по быстродействию управление для общего случая нелинейного объекта, описываемого уравнением (11.25), имеет релейный характер. Для линейного объекта уравнения (11.24) принимают вид п dxildt = Y aiixj + °{и, « = 1, 2, ... , п.(11.28) /=1 Сопряженные уравнения, согласно формуле (11.21), п dJdt = — Y kdVk/dXi. Учитывая, что dV>/dxi = -акт ("тг)= -dir (,ад + = сопряженные уравнения примут вид п dXfJdt = — Y= 1» 2, ... , п.(11.29) Если все корни характеристического уравнения объекта, соответствующего дифференциальным уравнениям (11.28), вещественны, то и все корни характеристического уравнения, соответствующего сопряженным уравнениям (11.29), также вещественны. Решение уравнений (11.29) в этом случае имеет вид суммы экспоненциальных составляющих %() = £ Cifea>\(11.30) где а,- — вещественные числа (корни характеристического уравнения), Ctf — постоянные интегрирования (начальные значения экспонент). В соответствии с формулой (11.27), оптимальное управление в слу-fV чае линейного объекта определяется выражением> п пп и = t7raax sign Y bt Y Cifea = t7max sign Y Bfi"1, (11.31) «=i /=i/=i n где В, = Y bid,. Поскольку сумма n экспонент, входящих в формулу (11.31), может переходить через нуль не более (п — 1) раз, то число интервалов управления будет не более п, что и требовалось доказать. В том случае, когда ограничено не только управляющее воздействие и, но еще и некоторые промежуточные переменные, число интервалов k оптимального управления будет больше п [81]: k = [(n — m)+ l][(m— 0+ 1] ••• —1,(11.32) где п — порядок характеристического уравнения объекта, связывающего хси;пг,1 — порядок уравнений, связывающих х с соответству- 0 ... 118 119 120 121 122 123 124 ... 143 |












