Раздел: Документация

0 ... 117 118 119 120 121 122 123 ... 143

переходного процесса в реальных системах зависит от степени ограничения координат (нелинейностей) системы. Производные от внешних воздействий, обычно значительные по величине и кратковременные по длительности, ограничиваются элементами системы и не вызывают желаемого эффекта форсировки в переходном режиме. Лучшие результаты при решении задачи повышения быстродействия САУ при наличии ограничений дает управление, оптимальное по быстродействию.

Задача об оптимальном быстродействии явилась первой задачей теории оптимального управления. Она сыграла большую роль в открытии одного из основных методов теории оптимального управления — принципа максимума. .Эта задача, являясь частным случаем задачи оптимального управления, состоит в определении такого допустимого управляющего воздействия, под влиянием которого управляемый объект (процесс) переходит из начального фазового состояния Н в конечное К за минимальное время. Критерием оптимальности в данной задаче является время.

П",! решении частной задачи обеспечения минимума времени переходного процесса, как отмечалось, G (х, и) = /0 (х, и) = 1 и для определения Н можно воспользоваться формулой (11.10) вместо (11.11), а также n-мерным пространством вместо (п + 1)-мерного пространства. В этом случае уравнения движения объекта можно записать в виде

dxjdt = /, (х, и) = дН/di, i = 1.....п,(11.20)

а сопряженные уравнения (11.15) и (11.18) принимают вид

л

d/dt = — £ ipjdV,/dxt = — dHldxt, i =[,..., п. (11.21)

Пример 1. Управляемым объектом является двигатель постоянного тока, структурная схема которого изображена на рис. 11.15. Управляющим воздействием и является напряжение на якоре, а управляемой величиной х1 — угол поворота вала. Требуется найти управляющее напряжение, обеспечивающее поворот якоря двигателя за минимальное время от начального положения xt (О) = 0, dxl(0)/dt=0 в конечное положение хх (/к) = , dxx (tldt = 0. При этом на управляющее напря-

к

жение наложено ограничение и Llma%. Решаем задачу по плану, намеченному в п. 11.2.

1.В соответствии со структурной схемой записываем уравнение объекта

Тр2хг + рх1 = Ы, р = d/dt,

или

Тх1+х1 = ku.

Вводим обозначение хг — х2 и записываем уравнения объекта в виде уравнений первого порядка

х1 = х2= Vi, x2=-(l/T)x2 + (k/T)u=V2.

2.Находим функцию Гамильтона

п

Н = W = £ = + ф» I- (1/Г) х2 + (k/T) и]. f=l

---

	А		1 Р
f	Тр+1

Рис. 11.15. Структурная схема .двигателя постоянного тока.

3. Составляем сопряженные уравнения в соответствии с формулой (11.21):

<*ф

,Г , dVt , , dV2 1 Г

Г u dVt , и dV2 1 Г ,

dx2

= 0;

dx*

dx„

d(—x2/T + ku/T)

2dxx

(11.22)

d(— x2/T + ku/T)

(11.23)

В соответствии с сопряженным уравнением (11.22) фх = const = с\. Подставив значение ф, = Cj в уравнение (11.23), получим уравнение

решение которого

dyjdt — ф2/Г = — си

ф2 = С2 + С3е/г.

4.Подставляем полученные значения фх и ф2 в выражение для Н:

И = СЛ + (С2 + <V/r) (*и/Г — х2/Т).

5.Находим закон изменения ы, при котором Я достигает максимального значения, т. е. достигается оптимальность по быстродействию. Записываем условие оптимальности

Н = СуХь — (С2 -f С3е/Г) XzlT + (С2 + С3е/Г) ЫГ = max, откуда видно, что Н представляет собой линейную функцию переменной и и поэтому для определения и нет необходимости находить и приравнивать нулю производную dHldu. От управления .и зависит только третье слагаемое последнего выражения Ни = (С2 + С3е/Г) ku/T, поэтому Н = max, когда Ни = max.

Функция Ни будет максимальная при максимальном значении управляющего •воздействия:

если (C2 + Cset/T

U„

если (С8 + С3е//Г) < 0;

•или

U,

max sjgn = t/max »gn (С, + Сзе/Г),

т. е. оптимальное управление является кусочно-постоянной (релейной) функцией, принимающей значения ± t/max.

На рис. 11.16, а изображен график функции ф2 = = С2 + С3е/Г для случая С2 > 0, С3 < 0, а на рис. 11.16,6—закон изменения управляющего напряжения и, при котором обеспечивается оптимальное по быстродействию управление. Из рисунка видно, что кривая ф2 один раз меняет знак, следовательно, оптимальное управляющее воздействие содержит два интервала управления, в течение которых и = const = = ±t/max. В соответствии с физическим смыслом на первом интервале 0 / < tt управление и = Uma% обеспечивает разгон двигателя, а на втором интервале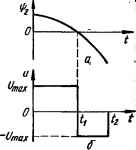

Рис. 11.16. График функции ф2 (а) и закон изменения управляющего воздействия (б).

---

f «g / < t2 управление и — —Uшах —• его торможение. В момент t2 двигатель останавливается. Методика определения моментов переключения tu t2 рассматривается в данной главе.

Теорема об и интервалах

Из рассмотренного примера следует, что для достижения максимального быстродействия необходимо на вход объекта подавать предельно допустимое управляющее воздействие, изменяющееся по релейному закону. Убедимся в этом на простейших примерах из физических соображений.

Пусть имеем апериодическое звено с передаточной функцией k/(Tp + 1), на входе которого управляющее воздейсгвие и ограничено по величине значением с/тах (П. 17, а). Такое звено может быть упрощенной математической моделью двигателя постоянного тока, на вход которого поступает напряжение, ограниченное значением а выходной величиной является угловая частота х = со. Требуется обеспечить изменение выходной величины (угловой скорости двигателя), например, от нуля до некоторого значения хсх за минимальное время. Если и = const, то при нулевых начальных условиях х (0) = 0 изменение х (разгон двигателя) осуществляется по экспоненциальному закону х = ku (1 — e~t,T).

Ясно, что для достижения возможно быстрого изменения х необходимо на вход звена подать предельное значение сигнала сУтах и удерживать его значение до момента tlt пока х не достигнет заданного значения хст (рис. 11.17, б). В момент времени tt следует мгновенно уменьшить и от Umax до ист = xCT/k, соответствующего установившемуся значению х = хст. Переходный процесс заканчивается в момент времени tt. При Т = const и хст = const длительность переходного процесса tt зависит от значения сУтах-

При подаче на вход интегрирующего звена с передаточной фунм цией kip постоянного по величине воздействия и (рис. 11.18, а) выходная величина звена изменяется по линейному закону х = kut. Для возможно быстрого изменения х от х (0) до хст следует, очевидно, на вход звена подать предельное значение управляющего воздействия " = Umax и поддерживать его до момента tlt когда х достигнет значения хст. В момент tt управляющее воздействие и необходимо скачком уменьшить от (Угаах До 0 (рис. 11.18, б).

и		К .	X

Рис. 11.17. Пример оптимального по быстродействию управления объектом, представляемым апериодическим звеном.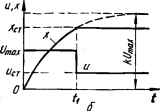

0 ... 117 118 119 120 121 122 123 ... 143