Раздел: Документация
0 ... 114 115 116 117 118 119 120 ... 143 I Рис. 11.10. Функциональная схема оптимальной системы. А у у р—J Объект Важным частным случаем оптимального управления является задача об оптимальном быстродействии. Среди всех допустимых управлений и = и (t), под воздействием которых управляемый объект переходит из начального фазового состояния хИ в заданное конечное состояние хк, найти такое, для которого этот переход осуществляется ва кратчайшее время. В этом случае подынтегральная функция G (х, и) = 1, а критерий оптимальности принимает вид 11.2. Методы решения задач синтеза оптимального управления ,Как следует из постановки задачи, при реализации оптимального управления и критерий оптимальности — функционал Q (х, и) =* G (х (t), и (t)) dt — принимает экстремальное значение. Обычно критерий оптимальности составляется так, чтобы условием оптимальности был минимум, когда Q (х, и) можно трактовать как обобщенную «стоимость» достижения цели управления, показатель «потерь». Задача определения оптимального управления и и оптимальной траектории х сводится к определению функции G (х (t), и (t)), которая придает функционалу Q (х, и) экстремальное значение. Если имеется несколько функций G (х (7), и (/)) и при одной из них функционал имеет экстремум, то эту функцию следует принять в качестве решения задачи. В случае сравнительно простых задач с одним или двумя управляющими воздействиями определение управляющего воздействия возможно методом прямого поиска путем многократного нахождения процесса на вычислительной машине при вариации управляющего воздействия. Метод динамического программирования Беллмана В основу метода динамического программирования решения вариационных задач положен следующий принцип оптимальности: участок оптимальной траектории от любой ее промежуточной до конечной точки также является оптимальной траекторией между этими точками. Например, если траектория /—2 между точками Н и К (рис. 11.11) является оптимальной, то оптимальным будет и любой ее участок от произвольной точки / до точки К. Справедливость прин- 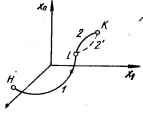 *2/ Рис. 11.11. К принципу оптимальности. ! ципа оптимальности очевидна: если траектория /—2 оптимальна (на ней достигается минимум критерия оптимальности), то оптимальной будет и траектория 2. В противном случае, если бы оптимальной траекторией между точками I и К оказалась какая-то другая траектория 2, то оптимальной траекторией между точками Н и К была бы траектория /—2, так как для нее критерий оптимальности имел бы меньшее значение, чем для траектории /—2 за счет меньшего приращения критерия на участке 2. Данный принцип оптимальности справедлив для систем, у которых оптимальная траектория не зависит от предыстории системы, а определяется лишь ее начальным состоянием. Суть метода динамического программирования поясним на следующем примере (рис. 11.12, а). Пусть требуется перевести некоторый объект из точки Н в точку К. Для этого необходимо сделать т шагов, каждый из которых, кроме последнего m-го шага, имеет I вариантов. Например, если в результате первого шага объект оказался в точке 1 вертикали 1, то для выполнения второго шага имеется I вариантов. Из точки 2 вертикали 1 второй шаг также может быть сделан в соответствии с одним из / вариантов и т. д. Для каждого варианта шага известна величина приращения AQt критерия оптимальности. В данной задаче число возможных вариантов траектории перевода объекта из точки Н в точку К равно числу комбинаций Г1-1. Из этого числа возможных траекторий требуется определить оптимальную траекторию (оптимальное управление движением объекта), соответствующую минимальному критерию оптимальности Q. Пусть, например, требуется выбрать маршрут автомобиля, проходящий через заданные точки, на котором достигается минимум расхода топлива или времени движения. Оптимальное решение можно найти перебором возможных вариантов на вычислительной машине, однако при больших значениях т и I, что имеет место при решении большинства реальных задач, это потребовало бы чрезвычайно большого объема вычислений. Решение этой задачи упрощается при использо- 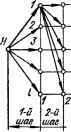 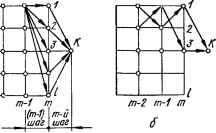 , а Рис. 11.12. К методу динамического программирования: а — пример задачи; б — определение оптимальной траектории. Таблица 11.1. К расчету оптимальной траектории
вании метода динамического программирования. Оптимальную траекторию этим методом, согласно сформулированному выше принципу, будем определять путем нахождения оптимальных участков траектории между точками некоторой промежуточной вертикали и конечной точкой К, постепенно переходя от точек одной вертикали к точкам другой в направлении от конечной точки К траектории к ее начальной точке Н. Сперва найдем оптимальные участки траекторий для перехода от каждой точки (т — 1)-й вертикали в точку К. Из точки 1 (т — 1)-й вертикали, как отмечалось, имеется I вариантов перехода в точку К: 1—1—К, 1—2—К, 1—3—К, .... /—I —/((рис. 11.12, а). Оптимальный участок траектории, дающий минимальное приращение AQ критерия оптимальности, можно найти • перебором из / вариантов или любым другим методом (методом градиента, методом наискорейшего спуска, методом Гаусса-Зейделя и др., которые будут рассмотрены в гл. 12). Пусть оптимальной траекторией, которой соответствует наименьшее приращение AQmin i, будет, например, траектория /—3— К (рис. 11.12, б). Результаты расчетов удобно занести в табл. 11.1. Из точки 2 (т — 1)-й вертикали к точке К можно перейти также по I траекториям. Аналогично находится оптимальная траектория (пусть таковой будет, например, траектория 2—/—К, рис. 11.12, б). которой соответствует наименьшее приращение AQmin 2 критерия оптимальности. Оптимальные траектории от всех других точек (т — 1)-й вертикали до точки К находятся таким же образом и результаты расчетов заносятся в таблицу или при использовании ЭВМ вводятся в память машины. При определении оптимальных траекторий между точками (т — 2)-й вертикали и точкой К учитываются полученные значения AQmin для последних двух (т и т — /) шагов и найденные ранее оптимальные траектории. Благодаря этому задача нахождения оптимальных траекторий между каждой точкой (т — 2)-й вертикали и точкой К упрощается и сводится к выбору оптимальной траектории из I траекторий. Случай, когда оптимальной между точками / и К является траектория /—2—/—К, а между точками 2 и К — траектория 2—1—3—К, иллюстрируется на рис. 11.12,6. Аналогично определяются оптимальные траектории из точек (т — 3)-й вертикали и т. д., вплоть до начальной точки Н. Для определения оптимальной траектории на последнем этапе необходимо найти минимальную сумму среди I сумм, составленных из приращений 0 ... 114 115 116 117 118 119 120 ... 143 |












