Раздел: Документация
0 ... 111 112 113 114 115 116 117 ... 143 ГЛАВА 11 Оптимальные системы автоматического управления 11.1. Постановка задачи оптимального управления Определение и необходимость построения оптимальных систем автоматического управления Системы автоматического управления обычно проектируют, исходя из требований обеспечения тех или иных показателей качества. Во многих случаях необходимое повышение динамической точности и улучшение переходных процессов систем автоматического управления достигается с помощью корректирующих устройств. особенно широкие возможности повышения показателей качества дает введение в САУ разомкнутых компенсационных каналов и дифференциальных связей, синтезированных из того или иного условия инвариантности ошибки относительно задающего или возмущающих воздействий 118, 22]. Однако эффект влияния корректирующих устройств, разомкнутых компенсационных каналов и эквивалентных им дифференциальных связей на показатели качества САУ зависит от уровня ограничения сигналов нелинейными элементами системы. Выходные сигналы дифференцирующих устройств, обычно кратковременные по длительности и значительные по амплитуде, ограничиваются элементами системы и не приводят к улучшению показателей качества системы, в частности ее быстродействия. Лучшие результаты решения задачи повышения показателей качества САУ при наличии ограничений сигнала дает так называемое оптимальное управление. Задача синтеза оптимальных систем строго сформулирована сравнительно недавно, когда было дано определение понятия критерия оптимальности. В качестве критерия оптимальности в зависимости от цели управления могут быть выбраны различные технические или экономические показатели управляемого процесса. В оптимальных системах обеспечивается не просто некоторое повышение того или иного технико-экономического показателя качества, а достижение минимально или максимально возможного его значения. Если критерий оптимальности выражает технико-экономические потери (ошибки системы, время переходного процесса, расход энергии, средств, стоимость и т. п), то оптимальным будет такое управление, которое обеспечивает минимум критерия оптимальности. Если Же он выражает рентабельность (к. п. д., производительность, прибыль, дальность полета ракеты и т. д.), то-оптимальное управление должно обеспечить максимум критерия оптимальности. Задача определения оптимальной САУ, в частности синтез оптимальных параметров системы при поступлении на ее вход задающего воздействия и помехи, являющихся стационарными случайными сигналами, рассматривалась в гл. 7. Напомним, что в данном случае в качестве критерия оптимальности принято среднеквадратическое значение ошибки (СКО). Условия повышения точности воспроизведения полезного сигнала (задающего воздействия) и подавления помехи носят противоречивый характер, и поэтому возникает задача выбора таких (оптимальных) параметров системы, при которых СКО принимает наименьшее значение. Синтез оптимальной системы при среднеквадратическом критерии оптимальности является частной задачей. Общие методы синтеза оптимальных систем основываются на вариационном исчислении. Однако классические методы вариационного исчисления для решения современных практических задач, требующих учета ограничений, во многих случаях оказываются непригодными. Наиболее удобными методами синтеза оптимальных систем автоматического управления являются метод динамического программирования Беллмана и принцип максимума Понтрягина. Таким образом, наряду с проблемой улучшения различных показателей качества САУ возникает задача построения оптимальных систем, в которых достигается экстремальное значение того или иного технико-экономического показателя качества. Разработка и внедрение оптимальных систем автоматического управления способствует повышению эффективности использования производственных агрегатов, увеличению производительности труда, улучшению качества продукции, экономии электроэнергии, топлива, сырья и т. п. Понятия о фазовом состоянии и фазовой траектории объекта В технике часто возникает задача перевода управляемого объекта (процесса) из одного состояния в другое. Например, при целеуказа--нии необходимо антенну радиолокационной станции (РЛС) повернуть из начального положения с начальным азимутом рн в заданное поло-:, жение с азимутом 6К. Для этого на электродвигатель, связанный с антенной через редуктор, подают управляющее напряжение и. В каждый момент времени состояние антенны характеризуется текущим значением угла поворота р и угловой скоростью со. Эти две величины изменяются в зависимости от управляющего напряжения и. Таким образом, существуют три связанных между собой параметра р, со, и (рис. 11.1)., Величины р и со = d$/dt, характеризующие состояние антенны, называются фазовыми координатами, и — управляющим воздействием. При целеуказании РЛС типа станции орудийной наводки возникает задача поворота антенны по азимуту и углу места. В этом случае будем иметь четыре фазовые координаты объекта и два управляющих воздействия. У летящего самолета можно рассматривать шесть фазовых координат (три пространственные координаты х, у, И и три компоненты скорости х, у, Н) и несколько управляющих воздействий (тяга двигателя, величины, характеризующие положение рулей вы- Объект Рис. 11.J. Схема объекта с одним, управляющим воздействием и двумя фазовыми координатами.
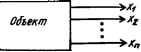 Рис. 11.2. Схема объекта с т управляющими воздействиями и п фазовыми координатами. Рис. 11.3. Схема объекта с векторным изображением управляющего воздействия и и фазового состояния объекта х.
соты и направления, элеронов). В общем случае в каждый момент времени состояние объекта характеризуется п фазовыми координатами xlt х2, хп, а к объекту может быть приложено г управляющих воздействий иь и2, щ (рис. 11.2). Под переводом управляемого объекта (процесса) из одного состояния в другое следует понимать не только механическое перемещение (например, антенны РЛС, самолета), но также требуемое изменение различных физических величин: температуры, давления, влажности кабины, химического состава того или иного сырья при соответствующем управляемом технологическом процессе. Управляющие воздействия иг (t), u2(f), ur (f) удобно считать координатами некоторого вектора и = (и1г ы2, щ), называемого вектором управляющего воздействия. Фазовые координаты (переменные состояния) объекта х1г х2, хп также можно рассматривать, как координаты некоторого вектора или точки х = (хг, х2, .... хп) в n-мерном пространстве с координатами xlt х2, .... хп. Эту точку называют фазовым состоянием (вектором состояния) объекта, а л-мерное пространство, в котором в виде точек изображаются фазовые состояния, называется фазовым пространством (пространством состояний) рассматриваемого объекта. При использовании векторных изображений управляемый объект можно изобразить, как показано на рис. 11.3, где и — вектор управляющего воздействия и {и1у и2, ur), х представляет собой точку х (jcj, х2, хп) в фазовом пространстве, характеризующую фазовое состояние объекта. Под влиянием управляющего воздействия и {ulf и2.....иг) фазовая точка х (х1г х2, хп) перемещается, описывая в фазовом пространстве некоторую линию, называемую фазовой траекторией рассматриваемого движения объекта. Если состояние объекта характеризуется двумя фазовыми координатами х1г х2 (см. рис. 11.1), то речь идет о фазовой плоскости, на которой фазовая траектория изображается особенно наглядно. Пусть, например, при подаче постоянного по величине напряжения и на двигатель, представляющий собой апериодическое звено, угловая частота вращения его ротора со (f) = х, (г) изменяется по кривой, изображенной на рис. 11.4, а, а производная (ускорение) du>{f)ldt =xa(f) по кривой, изображенной на рис. 11.4, б. Тогда фазовая траектория х {t) имеет вид, изображенный на рис. 11.4, е. 0 ... 111 112 113 114 115 116 117 ... 143 |












