Раздел: Документация
0 ... 52 53 54 55 56 57 58 ... 177 В результате переменная и функция будут заданы в виде двух соразмерных векторов, по которым будет построен график (рис. 64). у(х) :=еХсоа(12х) х:=0,0.001..5 И J«> " О : 1С-5 2-10-Э 3 10-3 < 10-Д 5-10-3 7Щ-3 810-1 Рис. 6.4, Построение графика с использованием ранжированной переменной Работа непосредственно с векторами значений может быть безальтернативным способом задания графика в целом ряде задач того же программирования. Однако при этом могут возникнуть проблемы, связанные с недостаточно малой величиной шага. Так, например, в случае функций, имеющих точки разрыва, вполне возможна такая ситуация, что две крайние узловые точки будут соединены линией, в результате чего вид графика будет искажен (рис, 6.5), у(х):=—ж:—3,-2.99,. 2 1 + х -д -з Id 1.001 1.002 1.002 1.0ОЭ 1.003 1 003 1.003 200т -то-1 Рис. 6.5. Ошибка при построении графика Пк1одолеть такую проблему в некоторых случаях можно, просто уменьшив шаг ранжированной переменной (для рассматриваемой задачи, как, впрочем, и для многих других, этот ход окажется неэффективным). Для изображения кривых проблемных функций лучше используйте автоматическое построение графика, так как при этом трудностей с точками разрыва практически никогда не возникает. Способ же задания графика с ранжированными переменными стоит применять только тогда, когда исследуемая функция непрерывна, или в том случае, если быстрым способом воспользоваться нельзя, Использование способа построения графика с иомошью оператора ранжированной переменной имеет очень важное преимущество перед быстрым методом, поскольку позволяет задавать произвольным образом шаг между узловыми точками. Конечно, это, как правило, не совсем важно при отображении зависимости в виде кривой, ко является принципиальным условием качественного построения графиков других типов — гистограмм, диаграмм, кривой с отложенными ошибками. Для таких зависимостей расстояние между точками должно быть довольно значительным, иначе элементы, их образующие, просто сольются. А так как автоматически система задает шаг довольно малым, то единственным приемлемым способом задания нетривиальных графиков Mathcad является использование оператора ранжированной переменной. П осгроить график в Mathcad можно и по готовым векторам или таблицам данных, полученных, например, при эксперименте или выполнении лабораторной работы. Естественно, при этом векторы должны быть соразмерны. О том, как произвести более корректное построение графика по экспериментальным данным, мы поговорим в гл. 16 (в разделе, посвященном интерполяции). 6.1.2. Построение нескольких графиков В Mathcad на одну графическую область можно поместить до 16 кривых. Чтобы добавить к уже имеющемуся графику еще один, выполните следующую последовательность действий. 1.Установите курсор справа от выражения, определяющего координаты последнего ряда данных по оси Y (предварительно выделив его). 2.Нажмите клавишу «,», При этом курсор опустится на строку ниже и появится чистый маркер. 3.В появившийся маркер введите выражение для новой функции или имя функции. С помощью описанного метода можно построить графики функций одной переменной. Если же кривые, которые нужно отобразить на одной области, зависят от различных переменных, то их, полностью аналогично добавлению новых функций, следует ввести через запятую в нижний маркер а том же порядке, что и соответствующие им функции. Иногда возникает ситуация, когда в одной области необходимо отобразить графики функций, амплитуда изменения которых сильно различается на выбранном промежутке. Так, если попытаться максимально удачно настроить вид одной из кривых, варьируя пределы по оси Y, особенности поведения второй могут остаться незаметными при данных настройках. Подобных трудностей легко избежать, если задать требуемый интервал изменения функции, используя вспоногателыгую ось Y (Secondary Y Axis). Для этого дважды щелкните на графике мышью. В открывшемся окне Formatting Currently Selected X-Y Plot (Форматирование выделенной декартовой плоскости) на вкладке X-Y Axes (Оси X и Y) установите флажок Enable secondary Y axis (Задействовать вспомогательную ось Y). При этом в правой части графической области появятся три маркера; в центральном нужно указать вид зависимости, в крайних — подходящие пределы изменения. Как и в случае главной оси Y, по вспомогательной оси Y можно построить несколько графиков, правда, для функций, зависящих только от одной переменной — последней из указанных в маркере оси X. Отобразить в одной графической области можно и кривые, заданные совершенно различными способами. Так. например, нет никакой трудности в том, чтобы визуализировать совместно график, заданный с помощью ранжированной неременной, и график, определенный через таблицу значений (рис. 6,6), ft» :=cos(sin(x)) хт=-3,-2.999.. 3  6.1.3. Форматирование шкалы графика Внести изменения в вид координатных осей вашего графика можно, обратившись к специальной вкладке X-Y Axes (Оси X н Y) диалогового окна Formatting Currently Selected X-Y Plot (Форматирование выделенной декартовой плоскости). Открыть данное окно можно тремя стандартными способами. □Дважды щелкнув левой кнопкой мыши на области графика. □Вьгпо.чм ин команду Fornix!: ► Graph ► X-Y Plot Формат > График ► X-Y эавИСИИОсТь), □Воспользовавшись пунктом Format (Формат) контекстного меню графика. Для настройки вида осей на вкладке X-Y Axes (Оси X н Y) имеются три идентичных списки параметров (рис 6.7), nrflMHimi СштгпПу Srleclrd XV Mill X-Y Ajm I Trac« Ubell D*(ou>« FrmurYYArS Secmiar, Y Art I 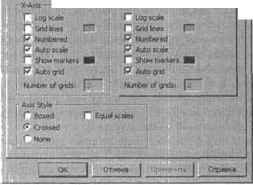 Рис. 6.7. Окно Formatting Currently Selected X-Y Plot (Форматирование выделенной декартовой плоскости] U Log Scale (Логарифмическая шкала). Если вы выберете этот параметр, то координаты по фор матируем ой оси будут прологарифмированы (но десятичному логарифму). Это может быть удобно в том случае, если значения координат точек вашего 0 ... 52 53 54 55 56 57 58 ... 177 |












