Раздел: Документация
0 ... 51 52 53 54 55 56 57 ... 177 □График кривой в двумерной декартовой системе координат (X-Y Plot). □График кривой в полярной системе координат (Polar Plot). □Поверхность (Surface), □Контурный график (Contour Plot). □Столбчатая трехмерная (3D)днаграмма(3 D Ва г Р to t), □Точечный трехмерный (3D) график (3D Scatter Plot). □Векторное поле (Vector Field), Всего же типов графиков в Mathcad - восемь, просто один из видов отображения трехмерной зависимости - так называемая «кусочечная* поверхность (Patch Plot) — не был вынесен на панель Graph (Графические). О том, как построить такой график, мы поговорим в разделе, посвященном форматированию трехмерных изображений. Аналогичный панели Graph (Графические) список всех типов графиков Mathcad расположен в одноименном ей подменю меню Insert (Вставить). Деление графиков на восемь типов очень условно, поскольку, изменяя различные параметры и установки, можно построить и не имеющую аналогов на панели или в меню Graph (Графические) зависимость. Так, например, изменяя тип отображения ряда данных в двумерной декартовой системе координат, можно построить не только тривиальную кривую, но и гистограмму, ступенчатый график и график с отложенными ошибками, Аналогично существу ют очень широкие, возможности форматирования и в трехмерной системе координат, Таким образом, можно смело утверждать, что типов графиков в Mathcad реально намного больше, чем восемь. В том, как суметь сориентироваться в этом многообразии и построить максимально наглядную кривую или поверхность, мы попробуем разобраться в данной главе. 6.1. Двумерные графики В данном разделе мы разберем особенности создания и редактирования изображений в декартовых системах координат, а также кратко затронем вопрос об особенностях задания полярных графиков. Кроме того, мы поговорим об использовании инструментов исследования двумерных кривых (трассировке и масштабировании). 6.1.1. Задание X-Y-зависимостей в декартовой системе координат В Mathcad существует несколько способов задания кривых в декартовой системе координат, однако первый шаг для всех будет один и тот же. Этим первым шагом является введение специальной заготовки для будущего графика — так называемой графической области. Ввести графическую область как для декартового, так и для любого другого графика можно либо с панели Graph (Графические), либо командой одноименного подменю меню Insert (Вставка). Также графические области имеют свои сочетания клавиш. Так, заготовку для декартовой двумерной системы координат можно ввести, нажав Shift+2. Графическая область представляет собой две вложенные рамки. Во внутренней отображаются непосредственно кривые зависимостей. Пространство между рамками служит для визуализации разного рода служебной информации. Графическую область можно увеличивать и уменьшать с помощью специальных маркеров, расположенных на ее внешней рамке. Перемещать по документу и удалять графические области можно точно так же, как иростые формулы. Окно форматирования вида графической области — Properties (Свойства) — также полностью совпадаете аналогичным окном для формул. Открыть его можно с помощью одноименной команды контекстного меню графика (вызывается щелчком правой кнопкой мышн на графической области). В окне Properties (Свойства) для подавляющего большинства пользователей объективно могут быть полезны два параметра, расположенных на вкладке Display. □Highlight Region (Цветная область). Установив этот флажок, вы сможете па палитре Choose Color (Выбор цвета) опредсл ить наиболее подходящий цвет заливки для вашей графической области. □Show Bonder (Показать границу). Параметр отвечает за отображение внешней границы графической области. По умолчанию она не визуализируется. После того itiiK фафическая область будет введена, в общем случае требуется задать два соразмерных вектора, определяющих значения координат точек. Сделать это можно различными способами. Наиболее простым и часто используемым методом задания координатной сетки является так называемый быстрый метод. При его применении пользователь задает только имя переменной и вид функции, а шкалы осей и величину шага между узловыми точками автоматически определяет система. Чтобы построить кривую функции по быстрому методу, выполните следующую последовательность действий. 1.Введите графическую область. 2.В специальном маркере, расположенном в центре под внутренней рамкой графической области, задайте имя переменной. 3.В центральный маркер, расположенный слева от внутренней рамки, введите функцию илн имя функции (если функцию определить раньше переменной, то работа даже упрощается, так как переменная будет задана автоматически). К недостаткам рассматриваемого метода относится прежде всего то, что область изменения переменной для всех функций определяется одна и та же; от -10 до 10. В большинстве же случаев такие пределы будут неприемлемы по целому ряду причин. Например, если мы хотим определить местоположение точек локального экстремума функции: «х) :-х5 - х3 + x2-3x-t 12 н используем для выполнения этой работы быстрый способ построения графика, тосис-тсмой будет прочерчена кривая, изображенная на рис. 6.2. Никакой полезной информации изданного графика почерпнуть неудастся, поскольку амплитуда экстремумов столь мала по сравнению с изменением величины функции на промежутке, что они становятся просто незаметными. Чтобы справиться с возникшими трудностями, нужно просто уменьшить интервал изменения либо переменной, либо функции. Для этого выделите графическую область щелчком левой кнопкой мыши. При этом визуализируются все элементы, которые до этого были скрыты. Непосредственно под крайними значениями (для оси X) ИЛИ слева от них (для оси Y) появятся цифры, отражающие максимальные и минимальные величины координат узловых точек графика. Чтобы изменить их значения, просто удалите (точнотак же, как при редактировании формул) старые величины и введите но- вые, Изменения пределов по оси X вызывает автоматический пересчет крайних значений по Y, Однако если вы переопределите область по оси Y. то область изменения переменной останется старой. 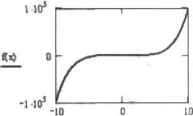 Рис. 0.2. График с неприемлемо большими пределами построения На практике же, как правило, приходится настраивать пределы сразу по обеим осям. Это связано с тем, что хорошо подобрать интервал по оси значений функции системе удается далеко не всегда. Исходя нз вышесказанного, попробуем произвести встройку вида графика рассматриваемой функции, изменяя диапазон как по оси X, так и по оси Y. Потратив немного времени на подбор наиболее удачных параметров, получим рис. 6.3. 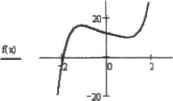 Рис 6.3. Конечный вариант графика для задачи на экстремум В ряде случаев (например, если в графике приходится очень часто менять диапазоны по осям) гораздо удобнее задать векторы данных самостоятельно. Сделать это можно с помощью оператора ранжированной переменной (вводится он либо с панели Matrix (Матричные), либо с помощью клавиши «;*). Чтобы задать вектор значений переменной с помощью оператора Range Variable (Ранжированная переменная), выполните следующую последовательность действий. 1.Введите имя переменной вместе с оператором присваивания. 2.Задайте левую границу интервала пекггроения и поставьте запятую. 3.Введите оператор ранжированной переменной. 4.В левом маркере введенного оператора задайте вторую точку на промежутке (тем самым вы определите шаг). 5.В правый маркер оператора ранжированной переменной введите значение правой границы на интервале. 0 ... 51 52 53 54 55 56 57 ... 177 |












