Раздел: Документация
0 ... 56 57 58 59 60 61 62 ... 177 Я*) l Ь ,1*10" -ш .- ID. Mn: -3.532S3 ] 0.756303 " Max: j 2 69461 1.697-58 ID 111. Рис.B.17. Использование инструмента Zoom (Масштаб! Y2 Cancel I -1  Рис. 6.16, Увеличенный фрагмент графика Если какой-то шаг при последовательном увеличении фрагмента кривой был сделан неверно, то вернуться на прельедуший этап масштабировання можно с помощью кнопки с изображением лупы с минусом в центре. Используя последнюю из трех кнопок, можно вернуться к первоначальному виду графика 6.1.10. Трассировка графиков Пожалуй, еще чаше, чем к инструменту масштабирования, приходится прибегать к использованию второго инструмента панели Graph (Графические) — Trace (Трассировка). При его помощи можно довольно точно определить координаты интересующей вас точки (например, корня или экстремума). Дли трассировки выполните следующую последовательность действий, 1.Выделите график и откройте панель инструмента Trace (Трассировка). 2.В результате на графике появится своеобразный «датчик» в виде пересекающихся штрихованных прямых (рнс. 6.19). Координаты точки пересечения этих прямых отображаются на панели инструмента в строках Х-, Y- и Y2-Value (Координаты по X, Y и Y2). Перемещать датчик можно, просто изменяя положение курсора. fix) :=х3-3х- 1 X-vabe I1,0ОД Copy x 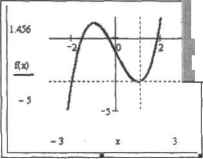 y-value Г2.9702 :opv v Y2-Valua P Track data pomts Copy Y2 Рис. в.1 В, Трассировка графика 3. Когда нужная точка будет найдена, нажмите кноггку Сору ХДЛ2 (Копировать X/Y/Y2), н (явисимости оттого, какая координата нас интересует. При этом ее численноезначение будет скопировано в буфер. Значительно облегчается работа при включенном параметре Track Data Points (Следовать точкам данных), так как при этом датчик инструмента Trace (Трассировка) будет скользить исключительно по кривой (см. рис. 6.19). Совместное использование инструментов панели Graph {Графические) позволяет весьма точно решать такие задачи, как определение координат корней, точек экстремумов, разрывов различных функций. 6.2. Зй-графики Со всей смелостью и ответственностью можно определить тему данного раздела — трехмерные графики (или ЗР-графикн) — как задачу недоступной для человека сложности. Конечно, очень легко проанализировать на предмет определяемых ими поверхностей такие классические уравнения, как уравнение шара, параболоида, эллипсоида. Но для зависимости нестандартной, тем более содержащей какие-либо специальные функции, построить поверхность вручную на бумаге очень сложно, практически невозможно. И если даже удалось бы определить координаты тех 500-1 ООО узловых точек, необходимых для задания среднего, более или менее гладкого трехмерного графика, то как их затем правильно спроецировать в объем, соединить и придать вид поверхности — это большой bonpocl Естественно, даже для человека очень незаурядных способностей и трудолюбия задача такал окажется практически не решаемой. С помощью же Mathcad такие графики можно строить очень просто, причем широкие возможности форматирования полученных изображений позволяют получать поверхности очень высоких художественных качеств. Тема 3D-графиков очень объемная и довольно сложная, она содержит множество методик, специальных функций и параметров. В данном разделе мы попытаемся прежде всего систематизировать это многообразие и на примерах продемонстрировать единый принцип, лежащий в основе всех способов построения трехмерных объектов. 6.2,1. Способы задания 3D-графиков Как уже говорилось выше, способов задания поверхности в Mathcad существует великое множество. Рассмотрим для начала наиболее простой и практически важный, быстрый метод построения трехмерного графика (GuickPlot). В его основе лежит тот же принцип, что и при быстром задании двумерной зависимости: пользователь определяет только вил функции, а все параметры построения, такие как шаг между узловыми точками, диапазон шкал осей и система координат задаются автоматически системой. Впрочем, даже быстрый метод в случае трехмерной системы координат имеет ряд тонкостей, поэтому ход построения этим методом поверхности рассмотрим по пунктам. 1.Для начала введем графическую область 3D-графика. Аналогично зависимостям X-Y, сделать это можно тремя стандартными способами: либо нажав кнопку Surface Plot (Поверхность) панели Graph (Графические), либо использовав одноименную команду меню Insert (Вставка), либо с помощью сочетания кчавнш Ctrt+2. Проводя аналогию с построением двумерной декартовой системы координат, вполне логичным будет предположить, что графическая область поверхности должна иметь три маркера для определения вида функции и ее переменных. На самом же деле маркер есть только один. В общем случае в нем должен быть прописан массив, содержащий координаты узловых точек но всем трем осям. Тому, как этот массив можно задать и что он собой представляет, и будет посвящен, во многом, данный раздел. Никаких принципиальных различий, кроме описанного выше, между графическими областями двумерных и трехмерных объектов нет. Поэтому на особенностях срор матирования графической области при га via ни н поверхности мы останавливаться не будем: оно абсолютно идентично двумерному случаю. 2.После тога как графическая область введена, следует задать вид функции, определяющей поверхность. В отличие от X-Y-эавиеимостей. просто ввести ее выражение и маркер нельзя — При этом будет выдано сообщение об ошибке: This variable is undefined (Данная переменная не определена). Мы будем строить поверхность следующей функции: f[xfy) :»«in(x+2y) 3.В маркер графической области следует ввести имя заданной выше функции. Однако, в отличие от двумерного случая, прописан должен быть лишь непосредственно текст имени, без переменных а скобках Это различие связано с тем, что трехмерный график, как уже говорилось выше, должен быть задан через массив данных, содержащий численные значения координат по всем трем осям. Вполне очевидно, что матрица с числами никак не может быть одновременно и функцией двух переменных. При быстром же построении поверхности мы имеем дело с таким же массивом, как если бы мы просто набрали его вручную, однако в данном случае параметры его определяются системой автоматически. Для рассматриваемой функции системой Machcad будет нарисован график, изображенный на рис. 6.20 При использовании данной методики поверхность задастся на стандартном интервале от -5 до 5 по обеим переменным. Естественно, такой диапазон во многих случаях может быть неприемлем (так, для нашей функции поверхность быстрого построения получилась слишком сжатой, что делает ее ненаглядной и неудобной для изучения). Изменить же интервал по выбранной оси так, как это делалось в двумерном случае, 0 ... 56 57 58 59 60 61 62 ... 177 |












