Раздел: Документация

0 ... 59 60 61 62 63 64 65 ... 177

динаты узловых точек, сама система при использовании изученного нами выше быстрого метода задания 30-графпка. Как вы помните, визуально разбиение интервала при этом легче всего представить в в>ие сетки. Через значения функции в узлах этой сетки и проводится поверхность. Математически же множество координат узловых точек сетки по каждой из осей можно представить в виде трех матриц. Нетрудно догадаться, что каждый отдельно взятый столбец матрицы X и каждая отдельная строка матрицы Y будет содержать одинаковые значения координат. Для того же, чтобы матрицы рассматривались совместно, нужно просто объединить их в один массив. Наиболее просто это можно сделать, введя имена матриц со значениями координат узловых точек через за пятую в маркер графической области (при этом они должны быть обязательно взяты в скобки).

	f\ 2	3		(\ 1			м	2	3
х>	1 2	3	Y:=	2 2	2		4	5	В
	J 2			,з 3					Ь

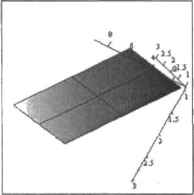Рис. в.27. Заданна поверхности, исходя из массива данных

Конечно, описанный способ задать поверхность может мало помочь при построении сферы, однако его стоило рассмотреть для того, чтобы в дальнейшем нам было легче разбираться в более сложных методиках. Тем более что при решении практических инженерных задач он имеет огромное значение, так как данные, например при автоматическом определении дефекта детали датчиком Холла организуются именно так, как это было сделано нами на рис. 6 27

Способ 2. Ранжированные переменные

Анатогично двумерному случаю, задать поверхность можно, используя оператор ранжированной переменной (что, как вы помните, аналогично заданию циклов в программировании). Так как с этим вопросом мы уже довольна хорошо знакомы но разделу о создании X-Y-графиков, то подробно на технических деталях останавливаться не стоит и мы сразу приведем пример задания сферы с помощью двух ранжированных переменных (рис. 6.28).

---

N:=20М:-20

i:«0.. Nj:=0..M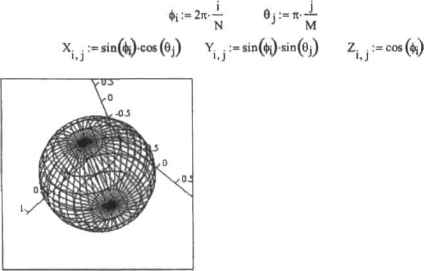

Рис. 6.2В. Задание сферы с помощью ранжированных переменных

Внимательно изучив предложенный алгоритм, нельзя не согласиться, что во многом данным способ повторяет те ходы, к которым мы прибегали, когда создавали график по готовым матрицам. Однако если вы попытаетесь открыть матрицу значении одного из уравнений, вы обнаружите, что все же есть одно принципиальное отличие: данные по координатам организованы не в виде матриц, а в виде векторов (рис. 6.29).

	0
20	0
21	0.309
" 22	0.305»
23	0.294 В
24	0,2751
25	□ .25 Ы
» 1

Рис. 6.28. Вектор значений уравнения для X

Различие это связано прежде всего с формой записи имени матрицы. Если сохранить индексы (что и было сделано), то по сути мы заставляем систему вывести каждый элемент в отдельности. Сделано это будет последовательным прочтением строк (слева

---

направо и сверху вниз - точно так же, как вы читаете эту книгу), В результате и получается вектор, фрагмент которого приведен на рис. 6.29. Однако в обишй массив мы объединяем, если вы обратили внимание, названия координат без индексов. При этом данные рассматриваются именно в виде матриц (рис. 6.30).

					КНКНБ
	0	Q	ц	0	0
		0.309	0.305	0.294	0.275	0.25 I
Х>р.		П.ЯИВ	0.581	0.559	0.524	0,476 Щ
	Hi	□.609	0.799	0.769	0.721	0.655
		0.961	0,939	0.905	u6*7	0.769 Щ
	,1

Рис. в.30. Таблица значений координаты X для сферы

Итак, никаких принципиальных различий между такими, на первый взгляд, разными способами задания поверхности, как использование экспериментальных данных и ранжированных переменных, нет. Равно как нет их и между всеми остальными методами. В основе всех способов построения поверхности лежит одна и та же идея: создание вложенного массива, описывающего некоторую сетку разбиений. Зная это, всегда можно задать совершенно любую зависимость, даже не зная никаких специальных функций или ходов.

Объединить матрицы или уравнения в один массив можно еще до введения его в маркер фафической области. Таким образом, в нашем случае массив данных можно представить в виде:

	Y		[21,21}
			121 ЛЬ

Описанный способ имеет скорее теоретическое, нежели практическое значение в связи с тем, что в Mathcad существуют функции, значительно облегчающие построение параметрически определенных трехмерных графиков. Однако изучить его было весьма полезно для понимания тех механизмов, которые лежат в основе построения поверхностей в Mathcad. Тем более что построить таким образом несколько графиков — это лучший способ разобраться в особенностях организации данных в Mathcad, что очень важно, особенно при решении задач программными методами.

Способ 3. Использование уравнения полусферы

Аналитически сфера определяется уравнением X2+Y*+ Z-KA где R - ее радиус. Однако для того, чтобы задать какую-то поверхность уравнением, оно должно иметь стандартный вид: Z-fX.Y).

В случае уравнения сферы координату Z можно выразить как

Z(X,Y):=Jr2- X2- Y2

0 ... 59 60 61 62 63 64 65 ... 177