Раздел: Документация
0 ... 60 61 62 63 64 65 66 ... 177 щи как В первом случае уравнение задает верхнюю полусферу, во втором — нижнюю. Воспользоваться распространенным в математике сочетанием «плюс-минус» не получится, поскольку в Mathcad его никак нельзя отгредслить. Однако выход есть: поместим на одну графическую область сразу две эти поверх! юсти. Слившись, они дадут шар. Последовательность действий следующая. 1.Вводим два уравнения полусфер. 2.Задаем циклы для переменных и определяем область изменения X и Y от -R до R (или сразу строим график быстрым способом и необходимые настройки делаем с помощью параметров вкладки QuickPlot окна форматирования поверхности). 3.Строим график, Но на последнем этапе вдруг возникает проблема: поверхность не отображается и вы -дается сообщение об ошибке: Function must return real scalar (Функция должна возвра тать действительный скаляр). В чем же дело? Л проблема заключается в следующем. Как вы помните, при создании образующей сетки каждом)1 значению X ставятся в соответствие все возможные значения Y (и наоборот). При этом, с учетом заданной области изменения переменных, обязательно найдутся точки, сумма квадратов координат которых превысит квадрат радиуса сферы. При этом подкоренное значение станет отрицательной величиной, а так как Mathcad рассматривает все числа как комплексные, то координате Z в таких точках будет присвоено мнимое значение. Естественно, что построить при этом поверхность будет невозможно. Проблему можно было бы легко решить, если бы существовала возможность перехода от прямоугольной сетки разбиений к круглой. Но, к сожалению, в рамках данной методики это невозможно. Что же делать? Проявив немного фантазии, выход находим довольно оригинальный. Попробуем скомпенсировать недостатки системы ее достоинствами: используем широкие возможности работы Mathcad с комплексными числами. Для ограничения решений действительной областью воспользуемся функцией Re (от real - действительная), которая возвращает действительную часть комплексного числа. В нашем случае ее использование даст то. что мнимые значения координаты Z будут заменены на 0. Чтобы использовать вышеизложенную идею, уравнения полусфер переписываем в следующем виде: Попробуем теперь построить по полученным уравнениям сферу. Сфера наша получилась с недостатком в виде прямоугольной каемки (рис. 6 31). К сожалению, избавиться от нее никак нельзя. Она образована теми точками, мнимую часть которых мы заменили на 0. Но все равно, мы получили результат там, где получить что-то довольно трудно. Поэтому данную методику можно смело отнести К способам задания сферы в Mathcad, имеющим определенное познавательное значение. f](X.Y): = -f(X,Y)  f.fl Рис. в,31. Сфера, построенная по уравнениям полусфер с ограничением на мнимую часть Способ 4. Использование функции CreateMesh Довольно громоздкую запись параметрического задания сферы, рассмотренную и качестве второго способа построения, можно заменить более короткой и простой с помощью специальной матричной функции CreateMesh (Создать сетку). Алгоритм ее использования следующий. J. Задаем систему параметрических уравнений сферы: х(ф.9):=ящ(ф>сов(е) Y((M):=sin(<>>sin(e) г(ф,9):=со5(ф) 2. Объединяем матрицы данных в один массив: КФ.е) Вводим функцию CreateMesh (F,s0jl,t0,tl,s3rid,tgrid,f тар) в маркер графической области. Она имеет восемь пустых маркеров, в которые последовательно вводятся: •имя матрицы значений или функции F. Единственный обязательный параметр. Остальные могут быть определены как пользователем, так и заданы автоматически системой; •начальное значение первой переменной sO: •начальное значение второй переменной si; •конечное значение первой переменной tO; •конечное значение второй переменной tl; •число линий сетки по первой переменной sgrid; •количество линий сетки по второй переменкой tgrid; •карта отображения ftrtap. Что это такое, мы поговорим ниже. Для нашего случая параметры определяем следующим образом: CreateMesh(FA2jr,0,7i,50,50}. График построен. Согласитесь, такой способ — наиболее простой из всех рассмотренных, хотя и наименее наглядный для тех, кто не владеет системой Mathcad, Помимо поверхностей, параметрически в пространстве можно задавать и разного рода линии. Для этого существует специальная функция Create5rwce(F,tO,tl,tgrid,fmap) (Создать пространственные). Она имеет пять маркеров, в которые последовательно вводятся имя массива данных или системы параметрических уравнений, начальное и конечное значения параметра, количество разбиений промежутка параметра, карта отображения. В качестве примера использования функции CreateSpace приведем построение расходящейся спирали (в качестве типа графика следует выбрать Scatter Plot (График рассеяния) или Data Points (Точечный)) (рис. 6.32). r sin(l)t F(t):= cos(t)l Л t J 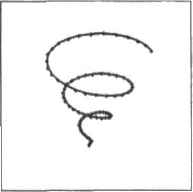 Ct*«l*Sptc*[F,0,6i,SG) Рис. 0.32. Использование функции CreateSpace Способ 5. Параметрическое закручивание Представим такую ситуацию: параметрических уравнений сферы вы не помните, а график с дефектами, получаемый исходя из аналитического уравнения, вас не устраивает. Что же делать? В такой сложной ситуации следует прежде всего хорошенько подумать и попробовать подойти к проблеме нестандартно. И решение будет обязательно найдено! Если вы знаете хотя бы уравнение окружности — этого уже вполне достаточно, чтобы решить поставленную задачу не только правильна, но и очень красиво. Впрочем, с помощью этого уравнения (аналогично случаю со сферой) мы сможем построить только половину окружности. Но и этого будет достаточно! Последовательность действий при использовании алгоритма параметрического закручивания следующая. 0 ... 60 61 62 63 64 65 66 ... 177 |












