Раздел: Документация
0 ... 67 68 69 70 71 72 73 ... 177 тового потока, падаюшеш на каждую точку малой, расположенной перпендикулярно линии, соединяющей ее центр н источник, площадки, будет одинаковым, При таком освещении проявляются эффекты теней и полутеней, однако нет бликов. * Specular Color (Зеркальный свет). Эффект освещения, получаемого от источника, расположенного на сопоставимом с размером поверхности расстоянии. Пример из жизни — прожектор освещения в театре. Свет падает круглым пятном, причем интенсивность его уменьшается от центрах краям. При этом для хорошо отражающих свет объектов проявляется такой оптический эффект, как блик. Степень яркости заливки поверхности определяется параметром Shininess (Яркость) вкладки Advanced (Дополнительные), По умолчанию освещение таким типом света не производится. Чтобы его задействовать, замените черный цвет в пат игре рассматриваемого параметра на любой другой. 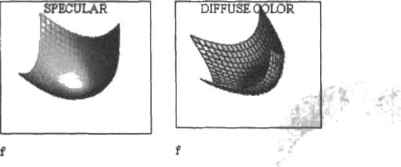 Рис. 8.58, Типы источников света □Infinite Light Source (Бесконечноудаленный источник света). Этот параметр отвечает за проявление эффектов, связанных с бесконечным удалением источника света. Определяет освещение диффузным светом. □Определить схему расположения источников света можно в списке параметра Lighting Scheme (Схема освещения). Вкладка Title (Заголовок) За задание заглавия графика отвечают параметры вкладки Title (Заголовок). Поместить название можно либо выше (Above), либо ниже (Below) поверхности. В том случае, если отмечен параметр Hide (Спрятать), название не отображается. Быстрое редактирование вида поверхности можно также провести с помощью ее контекстного меню (вызывается щелчком правой кнопкой мыши на области графика), которое содержит несколько наиболее важных параметров отображения. 6.2.3. Интересные поверхности Заканчивая разговор о построении н форматировании ЗО-грнфиков. рассмотрим несколько примеров оригинальных поверхностей, задаваемых с помощью систем параметрических уравнений. При изучении примеров обратите внимание на то. каких удивительных графических эффектов можно добиться, искусно используя возможности Mathcad в визуализации трехмерных объектов. Лента Мебиуса Лента Мебиуса является простейшей односторонней поверхностью, впервые описанной в 1865 голу профессором Лейпцитского университета Августом Мебиусом. Получается она при склеивании двух противоположных сторон прямоугольника, одна из которых перевернута. Лента Мебиуса (рис. 6.59) обладает замечательными свойствами: двигаясь по ее поверхности вдоль края в одном направлении, всегда попадаешь в исходную точку, но в обращенном положении относительно предыдущего; если же разрезать ленту Мебиуса по средней линии, мы получим не две части, а новую поверхность, аналогичную поверхности цилиндра, но пере крученную два раза вокруг себя.  Cte«tr>MesbrMoebiu» b«tiil,-J,2,-a 1,0.1,40,«Г) Рис. 6.50. Лента Мебиуса Поверхность Боя Поверхность Боя (рис. 6.60) — типичный представитель масса односторонних поверхностей (к которому, в частности, стюсится я знаменитая бутылка Клейка), которые невозможно отобразить в трехмерном пространстве без линий самопересечения (без самопересечения такие поверхности можно представить только в четырехмерном пространстве). (cos(u)-cos(2v) + y/2sin(u)cos(v))-cos(u) i/2 - sin(2-n)sin(3-v) (cog(u)-5Jn(2-v) -2sin(n)ain(v))cos(u) •J2 -&iii(2u)-sin(3-v) \fz cos(u)2 •Jl - sio(2u) ain(3v)  C«tt«M«»h(Bo3ri »urf»«.0,l.-».*.llM,lOO) с1«««Ш»ь(Вау« *иЛ«,0,2,-».п,100.100) Рис. 0.00. Поверхность Бое Сплетенная трубка Сплетенная трубка представлена на рис. 6.61. :-5 Ь-1Л5 с:=2 ш:-3 а?»5 (а + bcos(e) + c-sin(n-v))-cos(my)l (а + b-cos(e) + csin(ny )) sin(m у) b-ein(e) +• c-cos(n-\/) KnoUed tubc(9,\»);  ... .« < CtetteMesUKnottetlJubt, 0,10,0,10.200 Рис. 0.01. Сплетенная трубке Ракушка Ракушка представлена на рис. 6.62. а:=0.2 Ь:-1 с :-0.1 □ :=2 0 ... 67 68 69 70 71 72 73 ... 177 |












