Раздел: Документация
0 ... 69 70 71 72 73 74 75 ... 177 start —2 Ymd2 N:=l! M:= tl i := 0.. N j:=O..M Xend Xstart . Vj:-Ystart + end start j n t Чтобы легче понять дальнейшие шаги построения, разберемся, что такое векторное поле в принципе. В самом обшем случае векторное ноле - это вид графика, который описывает поведение функции двух переменных с помощью направленных стрелок векторов. В зависимости от того, какой математический (или физический) смысл положен в основу векторного поля, направление векторов и их величина могут вычисляться по-разному. Чаще всего в качестве такого базиса используется понятие градиента — вектора составленного из частных производных функции. В этом случае направление вектора поля определяется векторной суммой векторов отдельных частных производных в рассматриваемой точке (так как эти векторы параллельны соответствующим осям, то это предельно просто реализуется технически). Модуль же вектора поля определяется по теореме Пифагора как корень квадратный нз суммы квадратов частных производных. Математический смысл построенного таким образом графика довольно очевиден: направление стрелок характеризует поведение функции (возрастание или убывание), а также соотношение между приращениями по разным перемеи-ным, длина — быстроту изменения функции. В случае рассматриваемой задачи, аналогично построению векторного поля градиента функции, также требуется задать векторы, сложением которых будет определено направление векторов графика. Атак как модуль значения напряженности поля в любой точке пространства может быть легко вычислен, то очень просто можно задать необходимый базис, спроектировав вектор Е на координатные оси: Функния atan2(x,y) служит для вычисления угла между линией, соединяющей точку (х.у) и начало координат, и осью X. Впрочем, даже не прибегая к тригонометрии и не используя встроенных функций, можно догадаться, что соответствующие модули векторов базиса легко можно определить как: Никакой принципиальной разнипы от того, каким образом вы определите базис, не будет. Единственное, при задании ранжированных переменных следует учесть то, что в некоторых точках функция может не существовать. Так. в нашем случае нельзя задать М и N как 10, так как при этом придется вычислять значение функции в точке (0,0), что, естественно, невозможно. После того как координаты векторов базиса будут заданы, можно непосредственно строить векторное ноле (рис. 6.65). Для этого матрицы X и У объединяем в один массив (взяв их имена в скобки в маркере графической области).г В результате проделашгоЙ работы векторное поле получилось, и получилось правильно. Однако нельзя пе согласиться, что вид его, прн всей математической корректности. 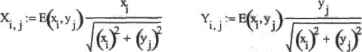 оставляет желать лучшего. Лишь четыре наиболее близких к заряду вектора имеют вид стрелки, остальные же столь малы, что отображаются в виде точки. Это связано с тем, что функция напряженности убывает очень быстро, а так как существует пропорциональность между размерами вектора поля и величиной функции в данной точке, то одни векторы оказываются несопоставимо болыи ими, чем другие. 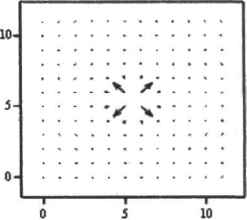 Рис. 6.65. Векторное поле (без логарифмирования) Чтобы решить возникшую проблему, вспомним, как мы справились с аналогичными трудностями при построении двумерных кривых. Тогда для этого была введена логарифмическая шкала. А что если попробовать прологарифмировать функцию напряженности? Ведь она как раз принимает только положительные значения: E(x,y):=log----,6 1/тс.Во х2 + 2 j Попробуем построить векторное поле теперь (рис. б".66). Согласитесь, что полученное векторное поле гораздо лучше того варианта, который был построен без использования логарифмирования. Кстати, меняя основание логарифма, можно сделать разницу между стрелками середины и краев графика значительной в той степени, в которой вы посчитаете нужной. Скажем несколько слов об о(рормлснии векторного поля. Из существующих возможностей оформления стоит выделить построение цветного графика и изменение толщины стрелок поля. Чтобы окрасить стрелки векторного поля выбранным цветом или палитрой, задействуйте параметр ПИ Arrows (Залить стрелки) вкладки Appearance (Вид). Толщинавекторов ноля регулируется с помощью параметра Weight (Толщина) меню Line Options (Параметры линии) вкладки Appearance (Вид). 6.3. Анимация графиков * 231 Также к векторному тюлю могут быть применить) все параметры вкладки Advanced (Дополнительные) и Lighting (Освещение). Однако нет смысла, например, окутывать векторное поле туманом или освещать направленным светом. 10- 04 Ч Ч \ Ч \ t f t f f * * ЧЧЧЧ t f t /* * * \ \ \ t / * * * * т.чЧ \ t f **** it тг 0510 Рис. б.вв. Вид векторного поля при использовании логарифмирования 6.3. Анимация графиков Вез сомнения, самой необычной, интересной и удивительной возможностью визуализации в Mathcad является анимация. В данном разделе мы кратко рассмотрим основные коды, применяемые при ее создании (более обстоятельный разговор невозможен по той причине, что просто в формате книг* очень и очень 1гро6лематично привести результат проделанной работы). Создается анимация в Mathcad точно так же, как, например, на студни Уолта Диснея. То есть она представляет собой быстро сменяющие друг друга кадры с более или менее значительными изменениями. А из-за того, что зрение наше довольно инертно, создается впечатление непрерывного процесса Требующиеся изменения в кадр вносятся с помощью специальной переменной FRAME (Кадр), Значение этой переменной равно по умолчанию номеру кадра, и, следовательно, может изменяться от 0 (до запуска процесса анимирования) до предельного значения 9999. Подставив переменную FRAME в функцию, вы заставите ее изменяться по мере того, как будут сменяться кадры (если увеличение переменной на 1 для каждого 0 ... 69 70 71 72 73 74 75 ... 177 |












