Раздел: Документация
0 ... 70 71 72 73 74 75 76 ... 177 кадра — это слишком много, то шаг можно уменьшить с помощью коэффициента). В результате при совмещении нескольких кадров получится анимация. Технические особенности задания анимации рассмогрим на примере следующей задачи: попробуем, меняя значение точки касания, заставнть касательную как бы скользить по кривой. Для этого выполняем следующую последовательность действий. 1.Задаем вид функции, касательную к которой мы заставим двигаться. Например: 3 2.Определяем начальное положение и шаг изменения точки касания при переходе от кадра к кадру. Проще всего это сделать непосредственно с иомошью переменной FRAME.: FRAME i t :=- + - 54 3.Задаем уравнение, описывающее касательную. В качестве точки касания определяем параметр с. ГХх) :=-у(х) dx tangem(t,x):=y(t) + D(0-(x-t) 4.Строим график функции и касательной. 5.С помощью команды Tools ► Animation ► Record Animation (Инструменты > Анимация ► Записать анимацию) открываем специальное диалоговое окно, содержащее параметры анимации. 6.Выделяем с помощью пунктирною прямоугольника (точно так же. как при масштабировании фрагмента кривой) ту часть рабочей области, которая должна быть отображена в анимационном ролике. Обычно выделяется только внутренняя часть графической области. 7.В меню For Frame (Параметры кадра) настраиваем параметры будущей анимации В окошке From (От) следует задать первое значение целочисленной переменной FRAME, в окошке То (До) — последнее. Количество кадров, сменяющихся в секунду, можно определить в окошке параметра АС Frames/Sec (Со скоростью: кадров в секунду). Для нашей задачи параметры должны быть определены следующим образом: FRAME изменяется от 0 до 30 со скоростью 10 кадров в секунду. В общем же случае, безусловно, шаг лучше делать по возможности более маленьким, а скорость прокрутки — высокой. При этом можно добиться очень высокого качества анимации, правда, лишь в том случае, если ваш компьютер достаточно мощный — иначе аы ими ро ванне будет производиться очень и очень долго. 8.Нажимаем кнопку Animate (Анимировать). При этом начнется непосредственно процесс аннмирования, за ходом которого вы сможете следить с помощью специальной зоны диалогового окна Animate. Количество проработанных кадров отображается подданной зоной в строке FRAME (Кадр) 9.После того как анимация будет завершена, на листе появится окно прокрутки видеороликов, нажав кнопку Play (Проиграть) которого, вы сможете просмотреть созданную анимацию (рне. 6.67). 6.3. Анимация графиков <. 233 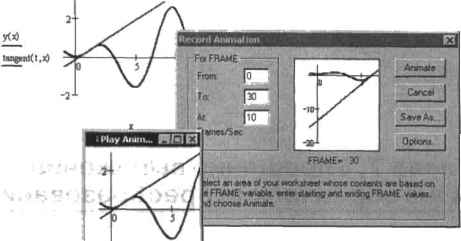 мм у——I Рис. 6.67. Просмотр созданной анимации I Созданные анимации можно сохранять с помощью кнопки Save As (Сохранить как) в стандартном видеоформате, что позволит просматривать их в дальнейшем и без использования среды Mathcad. Чтобы просмотреть созданную ранее анимацию с помощью Mathcad, задействуйте команду Tools ► Animation ► Playback (Инструменты > Анимация ► Воспроизведение). В появившемся окне прокрутки видеороликов нажмите кнопку Open AVI и выберите необходимый файл. Глава 7. Упрощение выражений и алгебраические преобразования Пожалуй, трудно найти более рутинную, однако и более часто встречающуюся математическую операцию, чем упрощение выражений. Практические любом выводе промежуточный результат приходится преобразовывать в форму, более удобную для дальнейшего использования. Разложение на множители, приведение общих слагаемых, переход от двойного аргументакодинаркому в случае тригонометрических функций — принципы проведения всех этих операций проходят еще в средней школе. Однако как не хочется порой терять время на то, чтобы, к примеру, в очередной раз перемножать полиномы или приводить две дроби к одному знаменателю! Значительную помощь при этом может оказать символьный процессор Mathcad. Конечно, наивно рассчитывать на то, что программа сможет без вашей помощи решать задачи уровня сборника М. И. Сканави. Однако проблемы логически менее нагруженные, но практически сколь угодно сложные с вычислительной точки зрения для нее вполне по силам. В этой главе мы научимся эффективно использовать возможности символьного процессора в области упрощения выражений, проанализировав на примерах, какие задачи можно полностью возложить на Mathcad, а в каких требуется ваше акгивное участие. 7.1. Разложение выражений Под разложением алгебраического выражения понимается математическое преобразование, переводящее степени и произведения в более простые для анализа суммы (например, (а-Ь)(а+Ь)-а1-Ь3). В случае разложения тригонометрических выражений функции кратного аргумента преобразуются в соответствующие им выражения от одинарного аргумента (например, sin(2:r)-2sin(x)cos(.r)); разлагаются также функции от суммы переменных (к примеру, по формуле sin(.v+)-sin(jr)-cos()+cos(.r>sin(#)). При разложении логарифмических выражений используются преобразования типа lri(a-o)-ln(a)+ln.(e), ln(o/U)-ln(a)-ln(6), logB(er)-j:. Для проведения разложения выражений в Mathcad существует специальный оператор expand (Разложить) панели Symbolic (Символьные). В левый маркер данного оператора заносится упрощаемое выражение, в правый —переметшая (или выражение), относительно которой разложение проводится. Объективно говоря, в подавляющем большинстве случаев заполнение 0 ... 70 71 72 73 74 75 76 ... 177 |












