Раздел: Документация
0 ... 19 20 21 22 23 24 25 ... 87 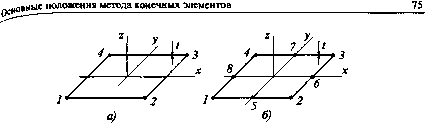 Рис. 3.14 Каждый узел имеет три степени свободы: О), в , в . Для каждого элемента лнней- •* У ные и угловые смещения можно выразить через функции формы следующим образом: co(x,y)=iNicoi; ex(x,y)=tNie ; 0y(x,y)=iNie i=li=7i=7 Как описано выше, для рассматриваемых элементов смещение (д(х,у) является линейной функцией для элемента с четырьмя узлами и квадратичной функцией — для элемента с восемью узлами. Глава 4 Практические вопросы и ответы В данной главе, составленной по материалам [8], при рассмотрении ряда вопрос ответов на них иллюстрируется практическое применение основных положений МКЭ. Вопрос 1. На приведенном ниже чертеже модели имеется 520 узлов и 800 прямоугольна конечных элементов. Из них 50 узлов жестко закреплены, а в 100 узлах фиксированы ремещения вдоль оси X. Какое количество неизвестных имеет эта конечно-элементная дель, если в каждом узле имеется по 3 степени свободы?  Ответ. Число неизвестных степеней свободы D — 3 • N — М, где N— число узлов! модели; М— количество известных степеней свободы. В данном пример! М = 3-50 + 100 = 250. Следовательно, D = 3-520-250 = 1310. Вопрос 2. Что преобладает в приаеденной на чертеже конечно-элементной модели: число элементов, число узлов, число степеней свободы, число кинематических граничных уел» вий?  Ответ: В данном примере: Элемент и: 660 • Узлы: 1095 I—• кинематические граничные условия: 14 Число неизвестных (степеней свободы): 3271 Число узлов обычно больше числа элементов; число степеней свободы в три больше числа узлов минус количество кинематических граничных условий. Таким о"» зом, в данной модели преобладает число степеней свободы. В каком случае размер задачи (число степеней свободы) максимальный (см. денные схемы): а) задача теплопроводности; 6) частотный анализ конструкции (пло-задача); в) прочностной анализ (трехмерная задача); г) прочностной анализ (оболо- « элементы)? Т,С а) б) в) Qmeem. Суммарное число степеней свободы определяется числом узлов и числом степе-jjfcBo6o,0bi в каждом нз них. Таким образом, суммарное число степеней свободы по вариантам: а) 50-1 = 50; 6)25-2 = 50; в) 20-3=б0;г)9-б = 54. Окончатель-Лий ответ: максимальное число степеней свободы в варианте в). ялпрос 4. Решение МКЭ показало, что сила F- = —ЮкН вызывает смещение в узле j, равное / мм. Какое смещение будет в узле i, если сила -20 кН действует в узле /? Fj = -20кН ы, = ? 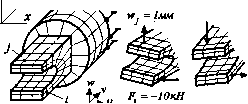 Ответ. В соответствии с МКЭ имеет место следующая схема вычислений: Матрица жесткости KKFt/wjiKjiFj/ui. Отсюда: и. = L . IF, V, = 7(~2Q) =2MM. На приведенном ниже рисунке показаны четыре варианта моделей с сеткой ко-jr™"* элементов: а) в одной н той же сетке присутствуют элементы первого н второго Lieu °В в °ДН0И и той же модели присутствуют линейные, балочные и оболочечные rtBJHTM; в) в модели присутствуют элементы с нулевой жесткостью; г) в модели прнсут-элементы бесконечно большой жесткости. 0 ... 19 20 21 22 23 24 25 ... 87 |












