Раздел: Документация
0 ... 18 19 20 21 22 23 24 ... 87 1/2 М = J X zdz (Нм/м); 39 -42 3)сдвиговые нагрузки (на единицу длины): t/2 О = f X dz (Н/м); х хг -t/2 t/2 Q = J T dz(H/m); У -1/2 У 4)максимальные изгибающие напряжения: 6М i \6М ( \6М v xmaxf2V ymax{2( Изгибающие напряжения достигают экстремальных значений при Z = +t/2. 3.7.2. Основные положения теории тонких пластин Тонкой пластиной называется такая пластина, для которой отношение толщины i1 другому характерному наименьшему размеру L (ширине или диаметру) менее 0,1. Если прогиб срединной плоскости мал по сравнению с толщиной пластины, то считают справедливым следующее допущение: нормаль к срединной плоскости до изгиба остается нормалью к этой плоскости и после изгиба. Как следствие этого можно заключить, что при изгибе тонких пласти отсутствуют деформации сдвига, т. е. у = у = 0. Обозначим через 0}(х,у) — прогиб срединной плоскости пластины, а через U,V — перемещения, паралле» ные осям Х,у соответственно (рис. 3.11). Для малых пр» гибов, когда углы наклона нормалей в каждой точке пласти-; ны приблизительно равиы тангенсам этих углов, можно за-. (Ц (3.49 С3.50) (3.51)1 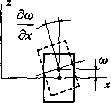 Рис.3.11 писать: U--Z- дсо дх V = -z- Тогда деформации составят: дсо д2 е - —г- д2 дх 2 со. а со £ =-Z--; у =-2z——~. у Ъу2 *у ЪхЪу (3.5SJ (3.5? Уравнения для напряжений в матричной форме можно записать следующим обр*3"1 (плоское напряженное состояние):I ху) 1-v
о о У I ху) X I ху > = —z- 1 * 1-v 1 v О v 1 О О 0 (1-v) д2со дх2 д2со ъу2 tf а со дхду (3.54) Таким образом, поле напряжений и деформаций определяется одной независимой переменной — смещением точек срединной поверхности Со( X, у). Уравнение равновесия тонкой пластины: DV4co = q{x,y), где D - (3.55) Et (ъ4 , э< + 2 — цилиндрическая жесткость пластины; ъ4 \ ; (](х,у) — распределенная нагрузка (Н/ м 2). [дх4 дх2ду2 ду4) Для сдвиговых нагрузок и изгибающих моментов можно записать: ШдМ дМ Q* дх (tf а со + ху М =D x дх + V ду д2со] Q = ху + ду2) ; М =D У Эх (tf а со Эу [ду2 + V со дх2 ) Решение дифференциального уравнения (3.55) требует учета граничных условий, в частности: защемление по контуру пластины — со = 0, = 0; ап Шарнирное опирай ие по контуру— со = 0, М -0; п свободная пластина — Q =0, М =0, пп где п — нормаль к границе пластины. 3.7.3. Основные положения теории толстых пластин дсо дх I со Рис.3.12 Ьу1н толщина / пластины недостаточно мала (tfL 1/10, где L — характерный lk,eP плнты), то такие плиты нельзя считать «тонкими». В этом случае 74 Часп, означает, что линия, перпендикулярная срединной поверхно пластины до деформации, не остается перпендикулярной этой поверхности после дефо мации (рис. 3.12). В этом случае новыми переменными являются в и 6 — углы клона линии, перпендикулярной срединной поверхности пластины до деформации, к осщ X и у соответственно. Оснонные соотношения: и = гв , v = -гв , Ух (3.56) е = z—-дх дв £y=~zt у -Z ху [Эу дх дй) а (3.57) 3.7.4. Конечные элементы для пластин и оболочек 3.7.4.1. Тонкий четырехугольный элемент с четырьмя узлами Схема элемента показана на рис. 3.13. Каждый узел имеет три степени свободы: СО,дсо/дх ,дсо/ду .Смещение Со{х,у) точек внутри элемента можно записать следующим образом: Ф.у)= Z i=l Срединная плоскость 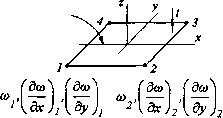 Рис.3.13 где N.,N .,N .—функции формы. I XI ух Матрицу жесткости для элемента по-прежнему можно записать в форме: [k)=\[B)T[E\B]dV. v 3.7.4.2. Толстостенный четырехугольный элемент Схемы четырехугольных элементов с четырьмя и с восемью узлами показана н3 рис. 3.14 а, б. 0 ... 18 19 20 21 22 23 24 ... 87 |












