Раздел: Документация
0 ... 15 16 17 18 19 20 21 ... 87 ftlarpHHa жесткости [ к ] — симметричная, т. к. симметричной является матрица Кроме того, заметим, что для данного материала матрица жесткости [ к ] зависит о от матрицы дифференцирования перемещений [в\. Матрица [В\, в свою очередь, толь* ясит от функций формы /V . Таким образом, то, насколько конечно-элементная модель if3 ет отражать свойства реальной конструкции, зависит от функций формы или, в конечном итоге, от вида (формы) конечных элементов. 3.2. Линейный плоский треугольный элемент Схема элемента показана на рис. 3.1. Элемент имеет три узла, перенумерованные против часо-joB стрелки. Каждый узел имеет две степени свободы, т. е. может иметь перемещения вдоль осей х и у. Предполагается, что смещения U, V любой точки внутри элемента являются линейными функциями координат этой точки: u = bJ+b2x + b3y; v = b, + brx + bv, 4 5 6 (3.16) где Ь., i = 1,2,...,6 —константы. Из (3.16), учитывая (1.14), можно получить выражения для деформаций: 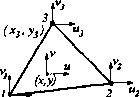 (хгУ1) Mi (Х2,У2) Рис.3.1 Ех = ди/дх = Ь2> 8 = oV/Эу = 6j, = ди/ду + Эу/Эх = b3+by (3.17) Из (3.17) следует, что деформации здесь не зависят от координат точки, т. е. являются постоянными в пределах элемента. В связи с этим такой линейных трехузловой элемент получил название «элемента постоянных деформаций». Заметим, что перемещения самих узлов также должны описываться уравнениями (3.16), при этом вместо X и у должны быть подставлены соответствующие координаты узлов (xit у,). Получим систему шести уравнений, из которой определим шесть искомых коэффициентов Ъ : i и1=Ь1+Ь2Х1+ЬзУ1 и2=Ь1+Ь2Х2+ЬзУ2 У3=Ь4+Ь5Х3+ЬбУ3-Репщв эту систему уравнений, получим выражения для Ъ,...,Ъ в зависимости от ""еремещений узлов и их координат. Окончательно для перемещений точек в пределах элемента получим: U N{ О N2 О N3 О О Nj О N2 О N3 где N. — функции формы (линейные по X, у ):
A = -det xi Уi X2 У 2 хз Уза где A — площадь треугольного элемента. Используя (1.14), (3.18) и (3.19), получим: 0.1 2А 23 32 13 32 У 23 Х13 У 31 Х21 У 21 12 где xij=xi ~xj yij =yi-Уи = 1.2>3 ) з) Из (3.21) следует, что деформации постоянны в точках внутри элемента, о чем уже ворилось выше. Следовательно, и напряжения в точках внутри элемента также постоянна Учитывая эти свойства данного трехузлового элемента, следует ограничить его прими* ние областями, где отсутствует большой градиент напряжений, т. е. вдалн от концентр торов напряжений. Этот элемент можно использовать для выполнения предварительны оценочных расчетов. Ос» основании (3.15) получим выражение для матрицы жесткости треугольного эле-прямолинейными границами (т. е. с тремя узлами): U]= \[Br\E\BW-«( [Bf[E][B] ).(3.22) V I толщина элемента. Заметим, что в этом уравнении [к ] — симметричная мат- "Lразмером 6x6. Как видно из уравнений (3.19), для плоского треугольного элемента в глобальной сис-к00рдинат X, у функции формы N. представляют собой достаточно сложные вы- теме 1 раже: ния. Эти выражения существенно упрощаются, если ввести локальную систему коор-данат > показано на рис. 3.2. Тогда функции формы могут быть записаны существенно проще: N2=t], N3=l-i-n. Заметим, что: N]+N2 + N3=J, (3.23) (3.24) t. е. условие (3.4 в) выполняется. 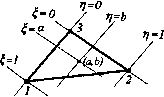 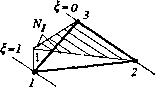 Рис.3.2 Рис.3.3 Отметим также, что функции формы (3.23) вдоль каждой из сторон треугольного элемента ведут себя точно так же, как и в одномерном случае (п. 2.1.1): N =7 в узле /; = 0 во всех остальных узлах и линейно изменяется вдоль стороны элемента. График изменения функции формы N приведен на рис. 3.3. Функции формы /V и /Vj ведут <*°* аналогично. Установим связь между глобальной {х,у) и локальной {£,Т)) координатными сис-1емами в случае плоских треугольных элементов. Соотношения между координатами да-1°та следующими уравнениями: x = N]X]+N2x2+N3x3 y = NIyI+N2y2 + N3y3 X = xi3i + X23ri + X3 или, иво.го, х.. = х.-х., уц = у.-у. = 1,2,3). (3.25) 0 ... 15 16 17 18 19 20 21 ... 87 |












