Раздел: Документация
0 ... 16 17 18 19 20 21 22 ... 87 Смещения U, V можно описать как функции координат глобальной {х, у) цщ кальной системы (,tj) координат. Известно, что перевод производных из локальн0> глобальную систему координат можно осуществить с помощью матрицы Якоби:
где [ J ] — матрица Якоби. Из (3.26) путем непосредственного дифференцирования получим: [J] = х13 У13 х23 У23. 1 2А У 23 У 13 х23 х13 где 2А = det [j ]= X у — X у (А —площадь треугольного элемента). 13£ щ*£313 Из (3.27), (3.28), (3.18) и (3.23) получим: дх ди 1 2 А Аи алогично: У -у 13 23 х13 dv дх dv L3yJ ди Эс: ди дц 1 2А 2А У У 13 23 х13 J и -и у23 -х у 13 23 х13 у1 ~v3 Используя (3.29), (3.30) и связь между векторами перемещений и деформаций (5 получим выражение для матрицы дифференцирования перемещений [ В ]: J 2А У 23 0 х 0 У3] 0 уп 0 32 х,з 0 21 х32 У 23 х13 У 31 х21 У12 Заметим, что это выражение для [ В ] полностью совпадает с ранее получение использованием глобальной системы координат (3.21). 3.3. Квадратичный треугольный элемент Перейдем к рассмотрению квадратичного треугольного элемента, схема которого по-а на рис. 3.4. В отличие от линейного треугольного элемента, элемент данного типа i>3Z*t 6 узлов: 3 узла расположены по углам элемен-в" j — по середине сторон. Каждый узел, как и инейиом треугольном элементе, имеет 2 степени goooflbi. В этом случае смещения ( U, V ) точек элемента должны выражаться квадратичными функциями их координат u = b,+b2x + b3y + b4x2 + b5xy + b6y2 v = b7 + b8x + b9y + b]0x2 +bjjxy + b]2y2 (3.32) где b. {i = 1,2,...,12) —константы. Из (3.32) легко вычислить деформации: ди 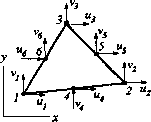 Рис. 3.4 дх = £x=b2 + 2b4x + Ь5у — = ey=bg+bux + 2bl2y ди д\ (3.33) Легко видеть, что в пределах данного элемента деформации являются линейными функциями координат. Таким образом, шестиузловой треугольный элемент позволяет более точно описывать поле напряжений и деформаций, чем рассмотренный в п. 3.2 трехуз-ловой треугольный элемент. В локальной координатной системе {,4]), которая полностью совпадает с введенной ранее в п. 3.2 для линейного треугольного элемента, шесть Функций формы для этого элемента можно записать следующим образом: Nl = № -1); N2 = rj(2rj -1); N3 = ф£ -1); N4=4&i;N5=4riG;N6=4& {£ = 1-§-tj). (3.34) Каждая из шести функций формы N. в (3.34) ВДяется квадратичной функцией локальных коор-нат но так же, как и в случае линейного трехуз-я°вого элемента, /V. = 1 в узле J и N. =0 — в ( ных узлах (рис. 3.5). смещаР°ЛЬЗуЯ ввеДенные в (3.34) функции формы, ЧеРе»ИЯ В Л10ои точке элемента можно записать смещения узлов следующим образом: «б и=22ХгЩ, v=£/V,vf. (3.35) i=li=l 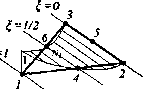 Рис. 3.5 68 .Часть, Матрицу жесткости для элемента по-прежнему можно записать в фор, [& ] = J[fi]7[iflfi]*/F, ио здесьбудет иметь квадратичную зависн V мость от координат X, у. 3.4. Линейный четырехугольный элемент Линейный четырехугольный элемент, схематично изображенный на рис. 3.6, пред, ставляет собой в системе локальных координат (,7?) прямоугольник с четырьмя узлалц в его вершинах. В системе локальных координатфункции формы записывают следующим образом: Nj =-(i-ai-ri); n2 =-{i+ai-n); 44 N3=Ul + ai + Tl);N4 =Ul-4Xl + r}); 44 4 Заметим, что, как и для ранее рассмотренных элементов: £ N. = J. i=l 1 Puc.3.6 Поле смещений задается следующими уравнениями: Рис. 3.7 (3.36) 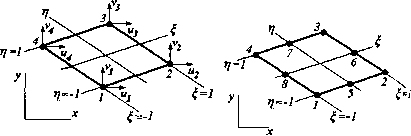 i=li=l Как следует из (3.37), и и V являются билинейными функциями в пределах seen элемента. 3.5. Квадратичный четырехугольный элемент Квадратичный четырехугольный элемент (рис. 3.7) представляет собой пр«*10 угольник с 8 узлами: 4 узла по углам и 4 узла по серединам сторон. В системе локально координат , t]) 8 функций формы записываются следующим образом: 0 ... 16 17 18 19 20 21 22 ... 87 |












