Раздел: Документация

0 ... 17 18 19 20 21 22 23 ... 87

NJ	= ~0-tXri-№ + ri + l); 4	Ns
N2	= Ul+ib-lb-i + l); 4	N6
Ns	4	N7	=l2o+r,ii	-e)
N4	= ~(Z-lXr, + №-r, + l); 4	N8		V)"

8

Снова £ N = J в любой точке внутри элемента. /=/ f

Поле смещений определяется уравнениями:

88

m=£/V.m., v=i;/V.v.(3.39)

которые представляют собой квадратичные функции. Деформации н напряжения в точках в пределах четырехугольного 8-узлового элемента являются линейными функциями координат, что позволяет более точно рассчитать напряжения и деформации, чем с помощью 4-узловых элементов.

В заключение отметим, что применение квадратичных треугольных или четырехугольных элементов с шестью или восемью узлами соответственно позволяют моделировать тела с криволинейной границей, что повышает точность результатов моделирования.

3.6. Преобразование нагрузки

Помимо сил, которые в расчете можно трактовать как сосредоточенные, на элементы конструкции действуют также поверхностные силы (например, внутреннее давление) н объемные силы (например, вес). Как поверхностные, так н объемные силы являются примерами распределенной нагрузки, которая в соответствии с принципами метода конечных элементов не может быть непосредственно приложена к элементу, а должна быть трансформирована к узлам. Приведение распределенной нагрузки к узлам основано на сравнении энергии упругих деформаций. С использованием этого принципа в п. 2.2.2 сформулированы правила трансформации распределенных нагрузок для одномерных стержневых и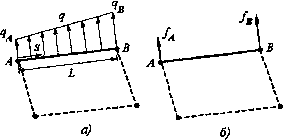

Рис. 3.8

---

70

52l

Рассмотрим правило трансформации поверхностной нагрузки, равномерно распр, леииой вдоль стороны четырехугольного элемента. Предположим, что лииейио распр леииая поперечная нагрузка д приложена к стороне АВ линейного четырехуголц элемента (рис. 3.8 а).

Введя локальную координату S вдоль стороны АВ, запишем выражение для рац W нагрузки Q:

W =t\u {s)q{s)ds,

q 0 п

где t — толщина элемента, L — длина его стороны, вдоль которой приложена нагру д, U — величина составляющей перемещения, нормальной к стороне АВ приложу

я

нагрузки.

Для линейного четырехугольного элемента с учетом (2.5) имеем: 11» =

, S 1S

1— и , +—U „. l) пА I пВ

Линейная поперечная нагрузка q(s) также может быть описана аналогичной форщ.

Таким образом, для работы W получим:

[l-s/L s/L]\

(l-s/L)2 {s/Lll-s/D {[s/Lll-s/D (s/L)2

ds-	>
	Ы

lUnA UnB\

tL

= \u . и I — пА nB* ft

2 1 1 2

*в\

откуда находим вектор эквивалентной нагрузки в узлах (рис. 3.8 Ь):

I/.

tL 6

2 1 1 2

Ли

В частном случае, при q = COKSt, получим:

if

(3.«

---

Лля 1свадратнчных элементов (треугольных или четырехугольных) с промежуточным посредине стороны распределенная нагрузка перераспределяется не по двум узлам, ""вьиие описанном случае, а по трем узлам.

к3* диалогичным же образом приводится к узлам и распределенная нагрузка, касательная -аанице," объемная нагрузка. * Напряжения в точках элемента вычисляются по следующей формуле:

а x		е x
а	= [Е\	е •
У		У
X 1 *У\		У 1 *У.

(3.45)

Здесь [в] — матрица дифференцирования перемещений; {d}— вектор смещений узлов, которые должны быть известны для каждого из видов примененных элементов после решения глобальной системы уравнений.

3.7. Пластины и оболочки

3.7.1. Основные соотношения теории пластин и оболочек

Элементы конструкций плоской формы, весьма широко распространенные в строительстве н технике, принято рассчитывать как пластины. Пластиной называют плоское тело любой формы в плане, толщина которого мала по сравнению с другими линейными размерами. Расчетная схема элемента пластины приведена иа рис. 3.9. В нем выделяют срединную поверхность, параллельную внешним поверхностям, делящую толщину пластины пополам. Координата z в направлении толщины пластины, как правило, отсчитывается от срединной поверхности. Эпюры нормальных и ка-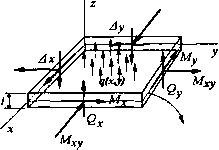

Срединная плоскость

Рис. 3.9

ительных напряжений представлены на рис. 3.10. Имеют место следующие вполне оче-виДные соотношения между нагрузками н напряжениями:

1)изгибающий момент (на единицу длины):

t/2

М = f a zdz (Нм/м);

х;, X

-t/2

(3.46)

t/2

М = [ О Z dz (Нм/м); У -1/2 У

(3-47)

2)крутящий момент (на единицу длины):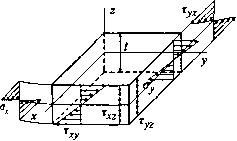

Рис.3.10

0 ... 17 18 19 20 21 22 23 ... 87