Раздел: Документация
0 ... 49 50 51 52 53 54 55 ... 78 Найти: Ах~В X =А~]В 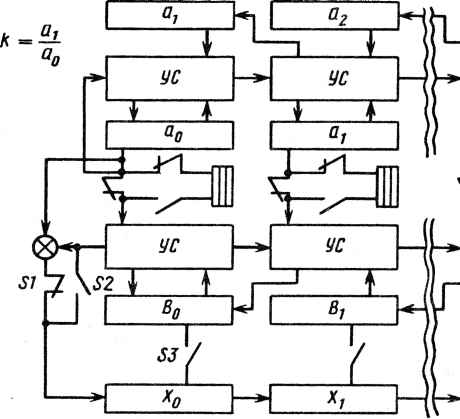 
Регистры Rr Процессор для умножения -сложения
Регистры Rг JliLrm Стек (магазинного типа) Процессор для умножения-сложения Регистры R. Регистры R, Рис. 17.8. Схема перемещения данных в решающем устройстве Теплица: УС - умножитель-сумматор ду этими двумя базовыми секциями находится стек, в котором хранится последовательность элементов матрицы U+ для дальнейшего использования. При получении СЛ по ВЛ-алгоритму рекурсивно обрабатываются строки А для получения вектора, обозначаемого символом А и используемого совместно со второй "вспомогательной строкой" А. На каждом шаге рекурсии вырабатывается "коэффициент отражения" К, характеризующий отношение первых элементов этих двух строк. По этому алгоритму последовательно перемножаются две данные строки так, что если вычесть одну из другой, то полученный результат А станет следующей строкой U+. При этом также вырабатываются новые вспомогательный вектор А" и коэффициент отражения. При инициализации решающего устройства регистры Щ и R2 загружаются элементами верхних строк А. Элементы матрицы В загружаются в регистр R3. В начале работы переключатель Sj замкнут, а переключатели S2 и S3 разомкнуты. Затем содержимое регистров R! и R2 подается на входы ВЛ-структуры, а результаты возвращаются в те же регистры. Новые значения А соответствуют последовательным строкам U*. Эти результаты одновременно запоминаются в стеке для дальнейшего использования и подаются на секцию обратной подстановки. В каждом новом временном периоде вычисляются новые значения А/, А , Ф/ и B;-s а промежуточные результаты запоминаются в регистре R4. Когда все элементы U+ будут вычислены и запомнены в стеке, сдвиговый регистр, содержащий промежуточные результаты , также будет заполнен. В этот момент переключатель Sx размыкается, S2 замыкается, а переключатель S3 замыкается на время, достаточное для загрузки в регистр R3 результатов ifij. Операции снова повторяются, и в каждый временной период вычисляется и запоминается в сдвиговом регистре новый результат Xj. ПЭ Данные В соседний процессор или из него
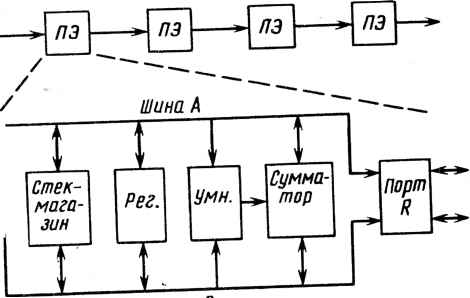 Данные В соседний процессор или из него Шина В 17.9. Процессорный модуль ориентированного на умножение процессора па СБИС  Рис. 17.10. Кристалл ориентированного на умножение процессора для конвейерной матрицы Функциональная схема, показанная на рис. 17.8, может быть далее приведена к конвейеризованному виду (рис. 17.9), позволяющему сократить объем аппаратуры. Необходимость такой процедуры обусловлена ограничениями, связанными с наличием у процессоров связей только с ближайшими соседями. Эти ограничения были продиктованы требованиями к скорости при одновременном снижении мощности, потребляемой драйверами глобальной шины. Схема основного процессорного модуля показана на рис. 17.10. Собственно кристалл содержит около 15000 элементов и обеспечивает длительность полного цикла обработки примерно 250 не. Среди этих элементов несколько необычных узлов, включая высокопроизводительный умножитель с ускоренным переносом, который обеспечивает время сложения, по существу не зависящее от длины слова. Это реализовано с помощью алгоритма Бута с основанием 4, при этом тактовая частота составила приблизительно 16 МГц [21]. В описываемом процессоре реализованы операции с фиксиро- 317
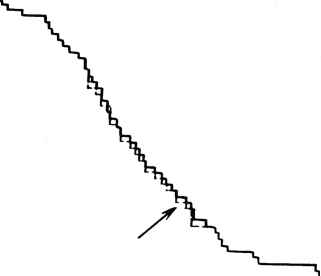 Ограничивающее переполнение 01- 0,00001 ли 0,000100,00100 0,01000 Погрешность округления о, юооо Рис. 17.11. Результаты программы моделирования - интегральное распределение 50 от счетов с фиксированной запятой при 16 секциях по Винеру-Левинсону (8.19) „ Ввод- вь/бод" ОУП с=0 ОУП „Ввод-вывод э □ □ р □ 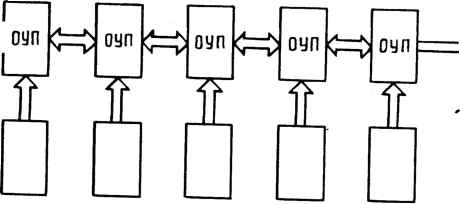 Память микропрограмм 1 Формиро-1 ватель адреса
Рис. 17.12. Функциональная схема платы процессора TOPSS-28, содержащего семь кристаллов ОУП ванной запятой при длине слова 28 разрядов. Такая длина слова получена в результате проведения обширной программы по моделированию, в которой использованы исходные данные из практических задач. При этом было осуществлено полное моделирование процессора, включая потоки данных, длину регистров и точность арифметики. Результаты, полученные для различной длины машинного слова, сравнивались с "бесконечной" точностью обра-ботки. По этим данным была рассчитана функция распределения погрешности (рис. 17.11) и определена оптимальная длина слова. Разрабатываемые кристаллы ориентированных на умножение процессоров будут собраны на печатной плате для образования полной теплицевской системы обработки TOPSS-28 (рис. 17.12). На плате скомпонованы семь одинаковых кристал-318 лов ОУП, дополнительных узлов деления, управления и тестирования, что позволяет обрабатывать матрицы размером до 16 X 16 приблизительно за 175 мс. Схемы проектировались на основе внутренней шинной структуры так, чтобы кристаллы ОУП могли соединяться непосредственно, что упрощает проектирование и изготовление платы. Полная система потребует встроенных средств для выполнения деления, которое является частью функций первой секции на рис. 17.12. По существу, необходимо вычислять величину, обратную 28-разрядному числу с фиксированной запятой за время около 1 мкс. Одной из возможностей является использование специализированных магистрально-ориентированных арифметических кристаллов или табличного подхода. В процессе работы контроллер платы должен генерировать 16-разрядный код операции для каждого из семи кристаллов ОУП с частотой 2 - 4 МГц. Одним из подходов к решению этой проблемы является использование ЗУ с формирователем адреса (счетчиком) в каждом из кристаллов. Данные в этих ЗУ можно рассматривать как микропрограммные процедуры. Каждый из формирователей адреса управляет микропроцессором, который должен иметь собственную память для машинных кодов. Для некоторых из задач микрокоды могут располагаться в ПЗУ, что упростит программирование до уровня выбора требуемой процедуры для каждого из кристаллов. Собственно плата, содержащая линейную процессорную матрицу, может работать в нескольких режимах по нескольким вариантам алгоритма Левинсона, различающимся сочетанием времени вычислений и объема памяти. Самый быстрый алгоритм требует OQt2) элементов памяти, решая уравнение АХ = В за 6п циклов. В другом варианте используется 0(п) элементов памяти, но время вычислений возрастает приблизительно до ISn. Рассматриваемый процессор выполняется по технологии, обеспечивающей разрешение 5 мкм, и содержит по одному процессорному элементу на кристалле. Однако при использовании более совершенной технологии число процессоров в кристалле и соответственно скорость обработки могут возрасти, как видно из табл. 17.2. Использование стандарта проектирования менее 1 мкм может обеспечить возможность построения однокристальной двумерной матрицы размером 25 X 25 элементов. Для следующей разработки рассматривается также вопрос реализации в кристалле процессора нескольких дополнительных средств для выполнения таких функций, как вычисление с плавающей запятой, извлечения корня и Таблица 17.2. Размеры процессора и время выполнения вычислений системой как функции от уровня технологии Размер элемента, Год выпуска Число процессоров в Время выполнения мкмкристаллевычислений, мкс 6197610,6 319814300,6 1198536100,0 0,25200057625,0 деление. В настоящее время рассматриваются проблемы технологической реализации такого проекта. Если удастся реализовать эти дополнительные средства, то окажется возможным обеспечить очень широкий спектр приложений в области АИРО, в особенности с двумерными структурами. К ним относятся одно- и двумерные свертки, коррекция с использованием метода максимальной энтропии, все виды двумерной фильтрации, аппроксимация сплайнами, геометрические преобразования для построения моделей и многое другое при скоростях вычислений, которые будут достаточными для большинства прикладных задач в реальном масштабе времени. СПИСОК ЛИТЕРАТУРЫ [1] М. J. Duff and S. Levialdi, Language and Architectures for Image Processing, Academic Press, New York, 1981. [2] Т. O. Binford, "Geometric Reasoning and Spatial Understanding," Proc. Image Understanding Workshop, Palo Alto, Calif., Sept. 15-16, 1982, pp. 18-20. [3] G. R. Nudd, "Image Understanding Architectures," Proc. Natl. Comput. Conf., Vol. 49, Anaheim, Calif., May 1980, pp. 370-390. Published by AFIPS Press. [4] A. Rosenfeld and A. Как, Digital Picture Processing, Academic Press, New York, 1976. [5] T. J. Ulrych and T. N. Bishop, "Maximum Entropy Spectral Analysis and Autoregressive Decomposition," Rev. Geophys. Space Phys., /5:183-200 (Feb. 1975). [6] K. Hwang, Computer Arithmetic, Principles, Architecture and Design, Wiley New York 1979. [7] M. J. Fiynn, "Some Computer Organizations and Their Effectiveness," IEEE Trans Comput., 27:125-140 (Sept. 1972). [8] M. J. B. Duff, "CLIP 4 A Large Scale Integrated Circuit Array Parallel Processor," Proc. 3rd Int. Joint Conf Pattern Recognition, 1976, pp. 728-733. [9] S. F. Reddaway, "DAP-A Distributed Processor Array," Proc. First Annu. Symp. Comput. Architecture, 1973, pp. 61-65. [10] К. E. Batcher, "Design of a Massively Parallel Processor," IEEE Trans Comput C-29{9) :836-840 (Sept. 1980). [11] I. E. Sutherland and C. A. Mead, "Microelectronics and Computer Science" Sci Am 257(3) :210-228 (Sept. 1977). [12] Карацуба А., Офман Ю. Умножители многозначных чисел на автоматах ДАН - 1962. - Т. 145, вып. 2 - С. 293, 294. [13] Milos Ercegovac, private communication, Apr. 1982. [14] W. K. Pratt, Digital Image Processing, Wiley-Interscience, New York, 1978. [15] N. Szabo and R. Tanaka, Residue Arithmetic and Its Applications to Computer Technology, McGraw-Hill, New York, 1967. [16] S. D. Fouse, G. R. Nudd, and A. D. Cumming, "A VLSI Architecture for Pattern Recognition Using Residue Arithmetic," Proc. 6th Int. Conf. VLSI Architecture, Design and Fabrication, California Institute of Technology, Jan. 1979, pp. 65-90. [17] H. T. Kung, "Lets Design Algorithms for VLSI Systems," Proc. Conf. VLSI Architecture, Design and Farbrication, California Institute of Technology, Jan. 1979, pp. 65-90. [18] S. Y. Kung, "Impact of VLSI on Modern Signal Processing," Proc. Workshop VLSI Mod. Signal Process., University of Southern California, Nov. 1982. 19] Фаддеева В. H. Вычислительные методы линейной алгебры. - М.: Гостехиздат, 1950 - 240 с. [20] N. Levinson, "The Wiener RMS Error Criterion in Filter Design and Prediction," J. Math. Phys. 25(4) :261-278 (1947). [21] M. D. Ercegovac and J. G. Nash, "An Area-Time Efficient VLSI Design of a Radix-4 Multiplier." Proc. Int. Conf on Computer Design, Port Chester, New York, Oct. 1983, pp. 684-687. 18 КРИСТАЛЛЫ СБИС-ПРОЦЕССОРОВ ДЛЯ МАТРИЧНОЙ ОБРАБОТКИ Р. Вуд, Г. Калл ер1, Э. Гринвуд, Д. Харрисон2 18.1.ВВЕДЕНИЕ В описываемом арифметическом устройстве обработки (А У О) используется 3-мкм кремниевая КМОП-технология фирмы Motorola и архитектура матричного процессора фирмы CHI Systems. Выбор архитектуры кристалла продиктован ориентацией на линейные векторно-матричные операции. Для такой обработки существует чрезвычайно эффективная архитектура. При архитектуре с одним умножителем может быть достигнута оптимальная эффективность при условии, что число шагов во внутреннем цикле программы ограничено числом операций умножения. Для любой области применения (распознавание речи, геофизика, радиолокация, томография и т. п.) матричные процессоры считаются весьма специализированными устройствами. Действительно, машины, которые спроектированы для решения конкретной задачи, являются таковыми; но важно то, что нами разработана архитектура, соответствующая алгебре билинейных форм. Она является основой матричной обработки и потому подходит для решения широкого спектра задач. В представленной здесь работе описывается самая последняя версия архитектуры семейства матричных процессоров [1, 2], которые были разработаны частично при поддержке управления перспективного планирования НИР Министерства обороны США. Более ранние варианты этого семейства процессоров образовали базис систем АР-120В [3]. В настоящее время при поддержке Министерства обороны США фирмы Motorola и CHI Systems разрабатывают СБИС-версию архитектуры, описанной в [4]. 18.2.ОБОСНОВАНИЕ ВЫБОРА МАТРИЧНОГО ПРОЦЕССОРА Чтобы убедиться в эффективности полученной архитектуры для произвольной матричной обработки, мы использовали набор таких задач, которые легли в основу выбора более ранних версий, и пересмотрели их с целью вклю- 1Фирма CHI Systems, Голета, Калифорния. 2Фирма Motorola, Скоттсдэйл, Аризона. 0 ... 49 50 51 52 53 54 55 ... 78 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||












