Раздел: Документация
0 ... 51 52 53 54 55 56 57 ... 78 be BXIXS BXlXS CI C0 XS BDECMUXS BTXS BUXS BVXSf >BXSO RS SYCL-ICL- 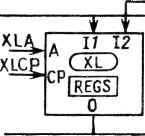 CLK cs* со*
CGRS "cos RI CO гшп R MCP YS XL MOP 1 А/ A2 AJ OP СЮ jMULT j 00 07 В/ B2 GCO >/7 YS SN FCO FOP A0 M CO ,-. CO A2 AJ OP ADD CI 0 JSNI I s CP f f COS CLK FCI ty ВТ О B2 BJ ZERpf f i A 0 LOGIC DP В TOP TCP II 12 OP CP GCO 16 GBSN GOP MPL GASN XS YL YS MPR AjTA/ 07 A2 AJ CO t ч СЮ CI 02 OP ГарТГ 03 В/ В? О B2 ВЗ zero}" 1 О IJI4- со U0P UCP GCI i 17 12 013 op Си""") CPffREG О IDECM I usz VS? CPf 17 "sz~l 0 SIZ VOP vc? Li i I/ 12 0IJ IopCO CP 2REG JL DSCL4 IF 17 flSP" 07 DSCLCP I CP LDSCL BSIZEXS BLSPXS Рис. 18.3. Архитектура АУО YAFOP Tyaeop 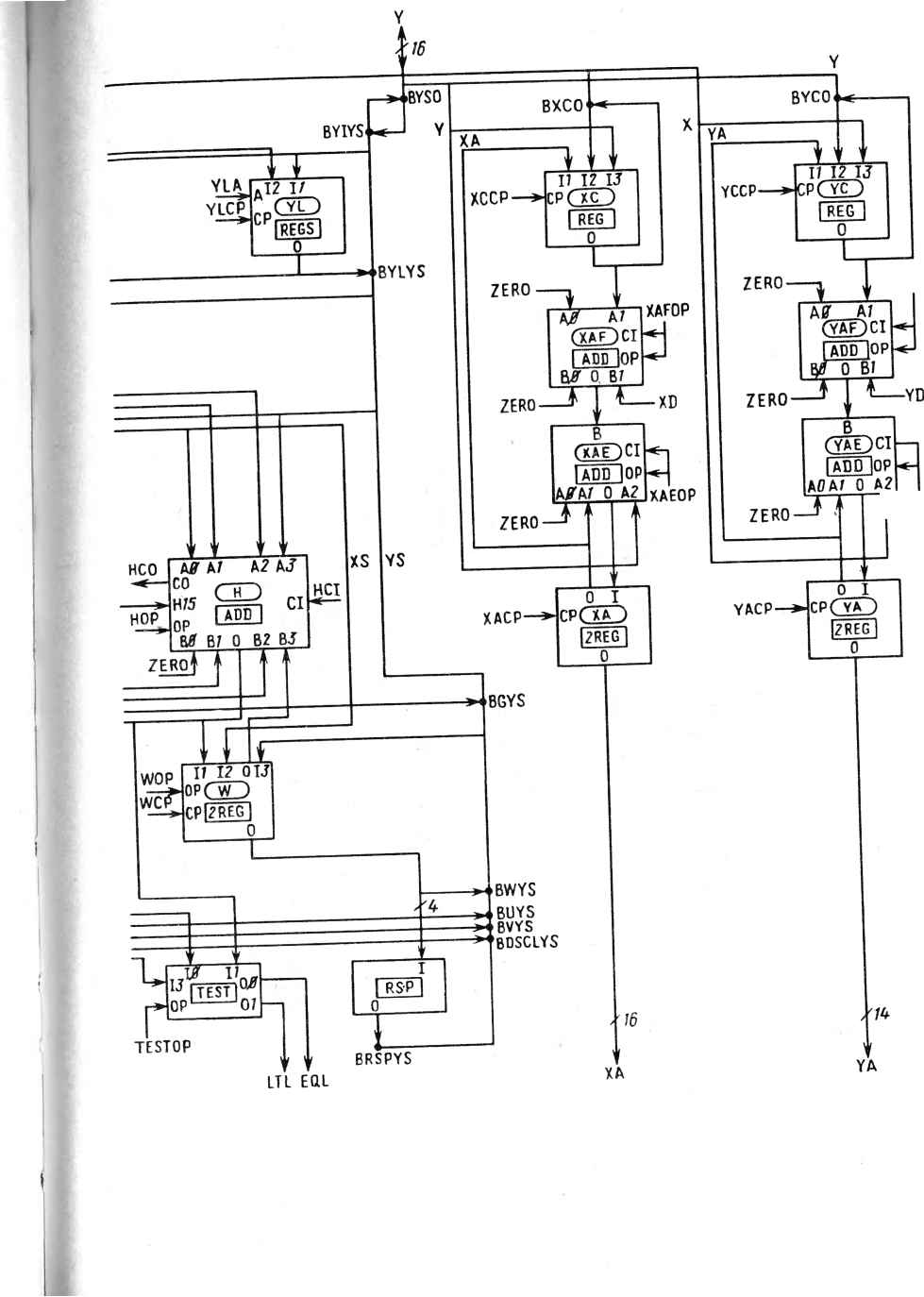 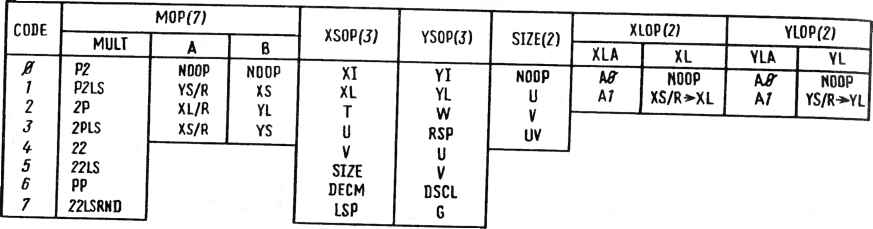
CODE T 7 2 3 4 5 6 7 10 11 12 13 lit-15 16 17 XAQPf4; noop xa=y inc xa(xd) dec xa(xd) xa=xc xa= y + xc inc xa(xc) dec xa(xc) xa = xc + xd xa = y+(xc+xd) inc xa(xc + xo) decxa(xc-xd) xa = xc-xd xa=y+(xc-xd) inc xa(xc-xd) dec xa(xc + xd) ХАСОРДО XCOPf2) noop xaxc x-xc xc Щ2) 1 2 3 4 yacop(4) noop ya=x incya(yd) decya(yd) ya = yc ya = x + yc incya(yc) decya(yc) ya = yg + yd ya=x + (yc + yd) ihcya(yc+yd) dec ya(yc-yd) ya - yc - yd ya-x + (yc-yd) inc ya(yc-yd) dec ya(yc + yd) YACOP(gj YCOPffl hoop yayc y yc xyc YDtfJ 1 2 3 4 Рис. 18.4. Коды микрокоманд АУО Может производиться и с%1)1ЧНое сложение. Могут производиться комбинации сдвигов RS, CS и обьпцнОГО СЛОжения на сумматорах G и Н, г:ак показано в поле SHIFT кодов ми кр0команд на рис. 18.4. Любые другие сдвиги в АУО производятся умножитлем посредством умножения данногС числа на соответствующую степень чи«сла 2? запоминания либо содержимого регистра MPL для сдвига вправо, либо pR дая сдвига влево, либо содержимого всего регистра MP для 32-разряднь 1Х операндов. Для указания необходимой степени числа 2 имеются два опертора (RSP и LSP) , описанные в следующем разделе. 18.5.2. Операции специальных функций Для повышения эффектрности алгебраической обработки массивов и арифметических операций с плавающей запятой имеется несколько специальных логических функций. ГяТЬ из эхих функций - унарные и называются RSP, DSCL, LSP, DECM и TE;sr Последний из операторов, называемый SIZE, дает разработчику микрокоманд возможность установить положение старшего разряда в массиве величин прошедших через регистр U, регистр V или полученных в результате ДизъоНКЦИИ содержимого этих регистров. :)Та функция полезна для групповых операций масштабирования чисел с главающей запятой. Логическая операцт 1Я JEST осуществляется с выходными результатами сумматора G, сумматор н или с их конкатенацией. Флажку Указывающие равно ли проверяемое чцсло нулю или оно меньше нуля, выведены из кристалла. Это средство подволяет ВЬШОлнять операции условного перехода по значению данных. Функц DECM выполняет 16-разрядное процеживание (разрядно-реверсивное) содерЖИМОГО регистра U с выдачей на ггшЫу XS. Эта функция полезна для вычиолсНИЯ аДресов при выполнении некоторых типов преобразований массивов ДнНых. Остальные функции описываются и иллюстрируются примерами в полеДуЮЩИХ подразделах. Основой оператора LSP Шляется операция "сдвиг влево для нормализации". Результат дает значен т счетчика, указывающего на сколько позиций произвести сдвиг (DSCL) ц степень числа 2, необходимую для выполнения этого сдвига (IS?). Оператор jjgp обрабатывает содержимое 32фаз рядной регистровой пары UV: если зНачение U отрицательно, то для вычисления результата LSP берется допол1штельныи код цу. Значение DSCL - пятиразрядное и представляет величину от q до 3i . Результат операции LSf> определяется старшими разрядами, следуЮЩИМИ за знаком, до тех пор, покР величина сдвига меньше или равна 15 противном случае результат LSPRyfleT определяться по 16 младшим разрдам Пользователь может определить, *сакой случай имеет место, проверив \)SCL. Результат LSP выдается на шИнУ XS, а величина DSCL - на шину YS >1ерез такт после получения результата LSP. В качестве иллюстрации использования этого оператора рассмотрим следующий пример . Предпол\)ЖИМ? чхо регистры U и V содержат мантиссу в ненормализованной дополш1тельиии форме со значением 1 Для удобства и большей НагЛЯдноети примеров формат АУО сокращу} вдвое, т. е. длина регистр013 составляет 8 Р%рЯДОВ> умножителя - 8 X 8 разрядов и т, д. иV 0001101101101101 Два нуля, следующие за знаковым разрядом (положительным), указывают что для нормализации результата в регистре UV требуется сдвиг влево на два разряда. Следовательно, результат операции LSP будет равен 00000100, а DSCL - 2. Нормализация содержимого регистров U и V выполняется следующими шагами: LSP.V:PP00000100 * 01101101 - LSP * U:Р200000100 ♦ 00011011 - MP >UV00000001 10110100 MPR + U >U01101100* . 01101101 10110100 которые дают правильно нормализованный результат. Когда требуется сдвиг на полное слово или больше, результат LSP получа-ется из содержимого регистра V, а не U. Предположим, что в регистрах U и V задана мантисса иV 0О000С0О 00010101 Те1юрьа знаком (положительным) следуют 10 нулей, которые означают, что ~ *U а величина Isp> полученная по содержимому регистра V имеет значение 00000100. Тогда шаги для нормализации будут такими- LSP * V • РР затем с соответствующей задержкой MPR - U и 0 ->V. Таким образом получим LSP.V:PP00010101 00000100 00000000001010100 MPR MPR -и. 0->V Uv 0101010000000000 что является правильно нормализованным результатом. Во всех предыдущих примерах рассматривались положительные числа. Предположим теперь, что содержимое регистров U и V имеет вид Uv 11110010 01010101 В этом случае оператор LSP предусматривает операцию дополнения значений U и V, так как значение U было отрицательно. Это дает следующий результат: COMPL:0000110110101010 и применение рассмотренного ранее алгоритма дает DSCL = 3, LSP = 00001000. Если оператор LSP применить к обработке содержимого регистров U и V, как в первом примере, то получим 332 LSP * V РР00001000 * 01010101 LSP * V РР00001000 .11110010 MP > UV00000010 10101000 MPR + U -> U+ 10010000 10010010 10101000 что является правильно нормализованным результатом. Во всех этих случаях следовало использовать значение DSCL для модификации порядка или для подсчета числа произведенных сдвигов. Оператор RSP используется в основном для выравнивания двух чисел с плавающей запятой перед сложением. Предположим, что регистры U и V содержат мантиссу, a W - положительную разность порядков. Тогда вызов RSP вырабатывает оператор умножения, который даст требуемый сдвиг вправо. Например, если регистры U, V и W содержат UVW 01001001 00100100 00000101 то требуемый сдвиг содержимого регистра UV вправо - пять разрядов, а RSP = 00001000. Операции выравнивания выполняются следующим образом: RSP * U :Р200001000.01001001 -- RSP.VPP00001000*00100100 - MP . UV00000010 01001000 MPL f V » V+00000001 *-- 00000010 01001001 что является правильно сдвинутым результатом. Этот метод пригоден также при обработке чисел с отрицательными мантиссами. Однако содержимое регистра W считается положительной величиной от 0 до 15 (от 0 до 7 в нашем примере при уменьшенном формате). Если значение W выходит из указанного диапазона, то для учета этого факта необходимо внести изменения в микропрограмму. 18.5.3. Средства условного сдвига Как уже упоминалось, во всех трех сумматорах, умножителе (MPL) и аккумуляторе U имеется дополнительный 17-й разряд, который обеспечивает проверку и коррекцию переполнения (1-разрядного) с помощью условного сдвига (CS). Этот дополнительный разряд позволяет корректировать переполнения, происшедшие в предыдущем цикле или на текущей операции. При переполнении значения 16-го и 17-го разрядов будут разными; в противном случае их значения будут одинаковыми. При выполнении сложения с условным сдвигом после операции сложения проверяется условие переполнения и при его наличии результат сдвигается на один разряд вправо. Условие переполнения фиксируется в регистре LGCO. Наличие 1 в этом регистре указывает на то, что сдвиг произошел, а 0 - что его не было. Таким образом, в следующем, за операцией CS цикле может быть сделано заключение о наличии или отсутствии сдвига. Представлены три случая, в которых используется операция CS. Первый - простая коррекция переполнения при сложении. Например, 333 0 ... 51 52 53 54 55 56 57 ... 78 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||












