Раздел: Документация
0 ... 32 33 34 35 36 37 38 ... 96 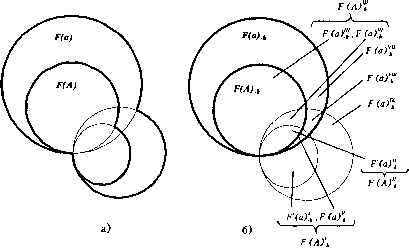 Рис. 2.3. Диаграммы Венна при исключении элемента ak из Я -множества цветов F(A)1 , существовавших в исходном ЯЛ5-множестве только за счет элемента ak, и исчезающих в F(A) k при исключении ak , соответствуют две зоны в диаграммах Венна: F(A) k =F{A) k л FA(ak)p = F{a)[k л F{a)\, (2.100) где цвета F(a)[k =F(a) k л FA(ak)p(2.101) не имеют одноименных цветов в F(a) k, и цвета F{a)\ =F(a) k л FA(ak)p л F(A) k,(2.102) для которых в F(a) k имеются одноименные цвета, но телом любого унитарного цвета, одноименного цветам F(a)k , как и F (a)! k > является только элемент ak. Поэтому здесь состав цветов F(A)r k отличается от состава вычисляемого по формуле (2.90) Группа цветов FiA)1 , существовавших в исходном ЯЛ5-множе- стве либо за счет ak и других элементов Д либо только за счет ak, здесь вычисляется не по формуле (2.91), а по формуле: F(A)nk = F (а)[1к = F(A) k л FA {ak )р.(2.103) В составе цветов F(a) k, одноименных унитарным цветам F(A) k , могут быть цвета, одноименные цветам F(ak ), не входящим в FA(ak)p, вычисляемые по формуле: Я*)™ =F(A) k л F(ak) л FA(ak)p.(2.104) Состав цветов, вычисляемый по этой формуле, в раскраске F(ak ) соответствует цветам FA(ak)N. Поэтому группа цветов F(A)rJ£, существующих в ЯЛ) и ЯЛ) £ только за счет других элементов, не считая исключаемый элемент ak, вычисляется по формуле: FU)777 = F(a)777 v F(<0™,(2.105) где F(tf)777 вычисляется по формуле: Яя)777 =F(A) k л F(ak),(2.106) соответствующей формуле (2.92). Группа цветов ЛЛ)7 , вообще не существовавших в раскраске Л Л) исходного Л -множества, а поэтому не существующих и в раскраске F(A) k множества IJAS k , вычисляется по формуле: ЯЛ)7[ =F(a)v FA(a),(2.107) где состав F-д (а) определяется по формуле F (а) = ЯЛ) л F(a). Поскольку, согласно (рис.2.36), Fj (а) = Яя)™ v F(a)VIkn v F(fl)™ ,(2.108) ТО ЯЛ)7[ = F{a) v F(e)™ v F(tf)777 v F(a)7* ,(2.109) где Fia)™ =FA(a)AF(ak)=F(a) k л?Ц)лШ)4, (2.110) FU)™7 =F(a) k AF(ak)AF(A) k AFA(ak)p,(2.111) F(a)7* =F(a) k AF(ak)AFA(ak)p.(2.112) В составе F(a) содержатся цвета из раскраски F(U) универсума, ие входящие в раскраски ни одного элемента исходного Я -множества. В состав F(#)77, F(#)777 и F(#)77 входят цвета элементов исходного /7А5-множества, не имеющие одноименных унитарных цветов в раскраске F(A)f при этом F(a)jf содержит такие цвета других элементов, исключая цвета F-д (ak ) элемента ak , Fia)11 содержит цвета, имеющиеся и в Fj(ak ), и в раскрасках других элементов, a F(a)1 содержит только цвета из раскраски FA(ak). При добавлении в свободное Я5-мпожество с составом компонентов (2.16) элемента ak, имеющего раскраску F(ak), получается новое множество: nS+k =(A+k,F(a)+k,F(A)+k,[A+k х F(a)+k], [A+k х F(A)+k],[A+k x A(F)+k]).(2.113) В отличие от операции исключения элемента из /75-множества, при добавлении в это множество нового элемента ak в получаемом множестве nS+k сохраняются составы всех элементов и цветов, существовавших в исходном Я5-множестве, и могут появиться новые цвета, обусловленные появлением нового элемента ak. Новые цвета могут появиться не только в F(a)+k, по и в унитарной раскраске F(A)+k из-за того, что появление ak может привести к появлению новых тел унитарных цветов. Поэтому элементы и цвета TIS+k связаны с элементами и цветами исходного Я5-мпожества соотношениями: A+k z> A; F(a)+k 2 F(a>, F(A)+k 2 F(A)\ A(F)+k 2 A(F). (2.114) Поскольку цвета разных элементов /75-множества при представлении их в составе F(a) и булевой матрице [А х F(a)] рассматриваются как независимые от цветов других элементов, способы вычисления компонентов F(a)+k и [A+k х F(a)+k ] нового множества (2.113) одинаковы для дизъюнктивных и конъюнктивных множеств. В исходном /75-миожестве состав цветов F(a) вычисляется по формуле (2.6). После добавления элемента ak состав цветов F(a)+k в новом множестве TIS+k вычисляется по формуле: F(a)+k =F(a)vF(ak),(2.115) или, при представлении всех цветов в едином булевом векторном пространстве (2.5), по формуле: F(a)+k =F(a)v F(ak).(2.116) Для построения булевой матрицы [A+k х F(a)+k ] в матрицу [А х F(a)] исходного /75-множества добавляется строка ak и столбцы, соответствующие новым цветам, появившимся в F(a)+k. Затем отмечаются элементы cky - 1, соответствующие цветам Fj е F(ak ), и построение матрицы [A+k х F(a)+k ] нового множества завершено. 0 ... 32 33 34 35 36 37 38 ... 96 |












