Раздел: Документация

0 ... 50 51 52 53 54 55 56 ... 96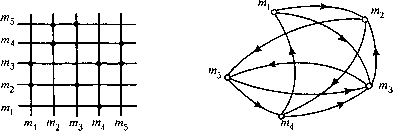

Рис.2.27. Представление графа па решетке и диаграммой

Использование критерия: количество технологических баз. Эта задача сводится к нахождению порядковой функции графа (рис.2.27).

Задание графа, по Бержу, делается при помощи соответствия Г между элементами и подмножествами множества М.

ГОи,)	= {т2,т3};
Г(т2)	= {тА,тъ);
Г(т3)	= {т2,т5};
ПтА)	= {тит3};
Пт5)	= {т3,тА}\
Пт{)	-» образ яг,

Граф можно рассматривать как пару G =(М,Г).

Граф G"1 определяется с помощью обратного отображения

г	-1;G-1	= (М,Г-1);
г	- \(тх)	= {т4};
г	-Кт2)	= {т2,т3};
г	-\(т3)	= {щ ,т4,т5
г	-\ЫА)	= {т2,т5);
г	-\(т5)	= {т2,т3).

Порядковая функция графа без контуров

Дай граф без контуров G = (М,Г), определим подмножества Nq, JV}, N2, Nq ={Xi / Х{ с М,Г~] (Х{) =0} т.е. берутся те вершины из М, от которых стрелки только уходят

---

N\ = {Х{ / Х{ с М - N0, Г"1 (Хг) с ЛГ0} - начинаются в ЛГ0.

Nr = {X, / X,- с М - ЛГ0 u Nx u...uNr !}

Г"1 (Xt) с ЛГ0 u Nt u...uNr t,

где г - такое наименьшее число, что Г(ЛГГ ) = 0, т.е. Nr состоит из вершин, к которым стрелки только подходят.

Подмножества Nk , k = 0, 1, ..., г образуют разбиение М и вполне упорядочены соотношением Nk<Nki<=>KK.

Функция О(Х), определяемая равенством Xj е Nk => O(Xj) = К, т.е. каждой вершине X, ставится в соответствие номер уровня К, называется порядковой функцией графа.

Рассмотрим построение порядковой функции графа на примере, используя алгоритм Демукрона: для графа механической обработки (рис.2.28) строим граф GT и Gz.

Строим граф G2 и GT. Образуем булеву матрицу: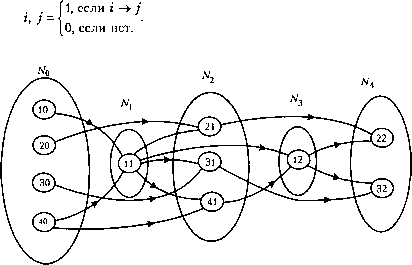

Рис.2.28. Разбиение графа GT на уровни

---

	10	11	12	20	21	22	30	31	32	40	41
10		1										V
и			1		1			1			1	V V
12					1				1			V V V V
20					1				1			V
21						1			1			V V V
22
30								1				V
31									1			V V V
32
40		1								1		V
41			1							1		V V V
АО	0	0	2	0	2	2	0	2	2	0	2
А1	X	2	2	X	1	2	X	1	2	X	1
А2	X	X	1	X	0	2	X	0	2	X	2
A3	X	X	0	X	X	1	X	X	1	X	X
А4	X	X	X	X	X	0	X	X	0	X	X

В строке АО нули - это вершины, из которых дуги уходят. Уровень N0 ={10,20,30,40} Уровень N\ ={11} Уровень N2 ={21,31,41} Уровень ЛГ3 ={12} Уровень NA = {22,32}.

Порядковая функция позволяет подсчитать количество ТБ и порядок их смены.

Если граф содержит контур, то обязательно, появится строка без нулей. Поэтому мы строим граф Gz u Gj*, т.е. одновременно с порядковой функцией определяем совместимость структур Gz и GT.

2.2.5. Разложение графа на максимальные сильно связные подграфы (приложение к задаче сборки или разузлования)

В некоторых задачах структурного анализа, т.е. где физическая (предметная) область моделируется графами, возникает проблема разбиения или разложения множества элементов системы на сильно связные подмножества. Для решения этой задачи нам потребуются некоторые определения.

0 ... 50 51 52 53 54 55 56 ... 96