Раздел: Документация

0 ... 51 52 53 54 55 56 57 ... 96

Транзитивное замыкание. Пусть задан граф G = (М,Г) (по Бер-жу). Определим многозначные отображения по формулам:

Г2Ы{)=Г{Пт{)}

Г3(тг) = Г{Г2(т()} = Г{Г{П?щ)}}

и обратные многозначные отображения по формулам: г-2Ы() = г {Г-1 Ои,-)}

Г-3(?щ) = Г"1 {Г"2(т,)} = Г"1 {Г-1 {Г-1 Ои,-)}}.

Пример: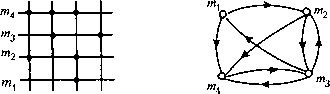

т\ т2 тз т4

Г(т\ ) = {m2, тА}, Г2 (mt) = Г(;и2 ) и Д *и4 ) = {т3, т4} Г3(т1) = Дт3) и Г(тл) = {т\ ,т2,т3,тА} Г"1 (wij) ={т3}) Г~2(тх) = Г-1 (w3) ={m2,;и4} Г~3(т\) ={ш1,т2,ш3}.

Очевидно, что Г72 (ти,-) и Г~п (wj,-) являются подмножествами тех вершин, в которые можно прийти из т используя пути длины п (или меньше), и тех вершин, из которых можно прийти в т, используя пути длины и (или меньше).

Транзитивным замыканием Г(т называется многозначное отображение, определяемое формулой

Г(т{) = {т{} и Дтя,-) и Г2(т{) и Г3(ш;)и...,

т.е. T{mj)- множество вершин, в которое можно прийти из тг по некоторому пути.

---

Аналогично определяется обратное транзитивное замыкание:

Г"1 Ы{) ={т{} и Г"1 Ы\) и Г~2(тх) и Г~3(тх )и...

т.е. множество вершин, из которых попадают в rrij по некоторому пути.

Л/жмер: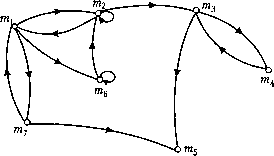

для приведенного выше графа. ТЫ\) ={m2,m6,m7Y, Г2(тх) = {тит2,т3,т6,т5} Г3 Ы\) = {т2 ,т6,т7 ,mum3,mA,ms} = М = Г(тх) Г~1(ш1) = {тт7}\ Г~2(тх) ={wt ,?п2,т6} Г~3(?щ) = {m2lm7imx ,m6} Г~А(т\) ={т/г2,i ,т6,т7} = Г-1 (wt).

Сильно связный граф. Граф G=(M,T) называют сильно связным, если (VWj е М)Г(т() = М, т.е. для любых двух вершин m,, ту

такого графа существует путь, идущий из irtj в rrij.

Пример сильно связных и несильно связных графов: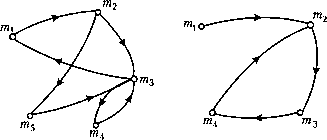

Сильно связный графНесильно связный граф

---

Приведенное условие эквивалентно условию: (Ут{ еМ)ГНт{)=М.

Разложение графа па максимальные сильно связные подграфы

Подграфом G графа G=(M,T) называется граф G = (M,r2), если М с М и (Vmj е М)Г2(т;) = MnT(mj).

Подграф G строится на подмножестве вершин графа G и включает все дуги, входящие и выходящие из этого подмножества.

Подграф называют максимальным сильно связным, если не существует сильно связного графа G", строго содержащего G.

Метод разложения графа на максимальные сильно связные подграфы

Если С(т() - подграф, содержащий т, то С(т{) = Г(т{) п Г"1 (ти,-). Метод состоит в следующем:

Берем произвольную вершину т и находим f(mj), f~x(m{) и Г{т{)пГ-х (mil

Затем берем вершину mj g С(т) и действуем аналогично. Процесс продолжается до тех пор, пока это возможно. Рассмотрим алгоритм на примере схемы сборки:

т2

комплекты

узлы

™5

			т7

В этом примере т3, т$, т§ - базовые детали. Преобразуем схему сборки в граф.

0 ... 51 52 53 54 55 56 57 ... 96