Раздел: Документация

0 ... 53 54 55 56 57 58 59 ... 96

Говорят, что задан абстрактный автомат, если задано:

1.X ={#,}, г = 1,/72 - входной алфавит;

2.У = {уу}, У = 1,77 - выходной алфавит;

3.Q ={qk), k = \,р - алфавит состояний;

4.F:X х Q ->Q - операция, переводящая декартово произведение F х Q в Q, или F X х Q -> (Q, У);

5.6fr g Q - начальное состояние автомата. Другое задание:

1. X ={Х{}У i =1,772

2.Y={yi},j = u 3.Q={qk),k=\

4. = f(x,q) - функция переходов.

5.у = \y(x,q) - функция выходов.

Перечисленные способы задания являются аналитическими. Они состоят из трех конечных множеств и двух функций, определенных на множествах.

Множества X, У, Qявляются не только конечными, но и счетными, эквивалентными натуральному ряду. Поэтому матричное задание автомата состоит в табличном задании функций q = f(x,q), y = \\i(x,q).

x\q	Я\	Я2		%	ЯР
*2
*i
хт

x\q	Я\	Я2		%	Яр
*\
*2
				Уг
хт

Геометрический способ задания автомата сводится к изображению ориентированного графа, вершинами которого являются состояния автомата, обозначаемые различными буквами: q е Q, а около каждого ребра (cjk , qj ставится буква входного алфавита лсг- е X, вызывающая переход автомата из состояния qk в qt, и буква выходного алфавита т/г- е У, которая появляется на выходе автомата. Если

---

автомат первого рода, то выходная буква определяется парой (qk х, а если второго рода, то парой Xj). Начальное состояние автомата обозначается буквой q\ е Q.

Таким образом, ориентированный граф, ребра которого нагружены буквами входного и выходного алфавитов, однозначно задает некоторый абстрактный автомат. Графы с нагруженными ребрами (весовыми функциями на ребрах) обычно называют графоидами. Поэтому ориентированный графоид - геометрическая интерпретация абстрактного автомата.

Пример способов задания абстрактного автомата.

Пусть задан абстрактный автомат (аналитическое задание):

А = (X, Y,Q,q = fix, q),y= i/(*f q)),

X ={xux2,x3), Y ={yx ,#2h Q={fl.<72.<73.<74} Функции f и \\f удобнее задавать таблично, отсюда табличный способ задания автомата:

L

x\q	71	72	7з	74
*\	71	7?.	74	7з
*2	Яг	7з	71	74
*3	7з	74	72	71

х \ q	71	72	7з	74
*\	У\	Уг	У\	Уг
xi	Уг	У\	Уг	У\
Ч	У\	У\	Уг	У\

Геометрический способ задания автомата: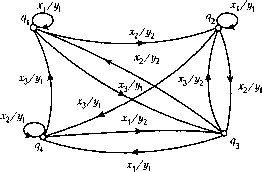

---

Предположим, что автомат является автоматом первого рода. Подача на вход автомата Д установленного в начальное состояние Ц\ входного слова Р\ = х\Х\х2х3х2х3 вызывает на выходе слово

Ц =У\У\У2У2У2У\-

Пример описания реального автомата абстрактным.

Из цехов А и В идут детали Л и Б в некоторой беспорядочной последовательности ААВАВВААВА... Требуется образовать тройки для последующей сборки (рис.2.29).

ААВАВВА...

ABA ABA ABA

Рис.2.29. Схема сборочного автомата

Х={хх = А,х2 =В); Y ={*/! =А*/2 =#>*/3 =°); 0={Я\>Я2>Яъ)-

qx - автомат ждет деталь А-Х\\

q2 - автомат А ждет В = х2;

<7з - автомат после АВ ждет А=Х\.

х2/0х/0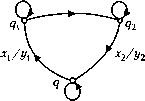

х2/0 Графоид автомата

		*2	У\	У2
	Я2	я<	Ух	0
ь	Яг	Яз	0	У2
ъ	Ях	Яз	Ух	0

Матрица переходов и выходов

2.2.7. Непрерывные модели

Представление технологической системы (ТС) в виде ориентированного объекта. Рассмотрим, от чего зависит погрешность каждого составляющего звена технологической размерной цепи. Для этого представим ТС в виде ориентированного объекта (рис.2.30).

х** - входное положение элемента формы заготовки, относительно технологической базы, свойства материала заготовки.

0 ... 53 54 55 56 57 58 59 ... 96